数据结构详解
2024.11.19 阅读量次数据结构是一门研究数据组织方式的学科,是编程语言的重要组成部分。学好数据结构,可以编写出更高效的代码,同时为学习和掌握算法奠定坚实的基础。
数据结构分为两大类:线性结构和非线性结构。线性结构是最常用的数据结构,其特点是数据元素之间存在一对一的线性关系。根据存储方式的不同,线性结构分为顺序存储和链式存储:
- 顺序存储:即顺序表,元素的存储地址是连续的。
- 链式存储:即链表,元素的存储地址不连续,每个节点存放数据和相邻节点的地址信息。
常见的线性结构包括数组、链表、队列和栈。非线性结构则包括多维数组、广义表、树和图等形式。
线性数据结构
常见的线性数据结构包括数组、链表、栈、队列和哈希表。数组是一种固定大小的元素集合,存储在连续内存空间中,支持快速随机访问。链表由节点和指针组成,能够动态调整大小,适用于频繁插入和删除的场景。栈遵循后进先出(LIFO)原则,通常用于处理递归和表达式求值等问题。队列遵循先进先出(FIFO)原则,常用于任务调度和缓冲区管理。哈希表通过哈希函数将键映射到固定数组位置,支持高效的查找、插入和删除操作,常用于实现集合和映射等功能。
| 数据结构 | 特点 | 优点 | 缺点 | 使用场景 |
|---|---|---|---|---|
| 数组 | 固定大小,元素存储在连续的内存位置 | 随机访问快速,内存使用紧凑 | 大小固定,不方便扩展,插入删除较慢 | 需要快速访问的场景,如查找、排序等 |
| 链表 | 由节点和指针组成,动态大小 | 动态调整大小,插入删除灵活 | 访问元素需要遍历,内存消耗大 | 频繁插入删除操作,如队列、栈实现 |
| 栈 | 后进先出,只在一端进行操作 | 操作简单,适用于递归和回溯问题 | 只能访问栈顶元素,存储空间有限 | 递归、表达式求值、深度优先遍历等 |
| 队列 | 先进先出,在两端进行操作 | 适用于排队和任务调度 | 只能访问队头和队尾元素,操作限制 | 任务调度、缓冲区、广度优先遍历等 |
| 哈希表 | 键值对存储,通过哈希函数映射到数组索引 | 查找、插入、删除操作高效 | 哈希冲突问题,内存消耗较大 | 实现集合、映射、缓存等功能 |
稀疏数组
稀疏数组是一种优化存储稀疏数据的数据结构。当一个二维数组中大部分元素为零或重复值时,可以使用稀疏数组仅记录非零元素的行号、列号及对应值,从而节省存储空间。
稀疏数组通过记录非零元素的位置信息和对应值,有效减少了存储空间的浪费,适合零值占多数的数据场景。它结构简单,适合序列化和持久化操作,占用存储资源较少。处理稀疏数据时,仅操作非零值,减少了无效计算,提高了数据处理效率。
稀疏数组需要记录每个非零元素的行号和列号,在数据密集的情况下,额外的存储开销可能超过普通数组。由于存储方式不同,操作稀疏数组时,如插入、修改和查找数据,复杂度会有所增加。对于密集数据,稀疏数组可能并不适用。
稀疏数组常用于记录棋盘类游戏的棋子状态,例如五子棋或国际象棋。它还适用于图像处理中存储稀疏矩阵,例如黑白图像的像素点数据。科学计算中的大型稀疏矩阵运算以及数据库中带有大量空白字段的稀疏表格也是稀疏数组的典型应用场景。
稀疏数组的第一行依次记录原数组一共有几行几列,有多少个不为零的值,之后的每行记录原数组中不为零的值所在的行数、列数以及数组中元素该值。如图所示:
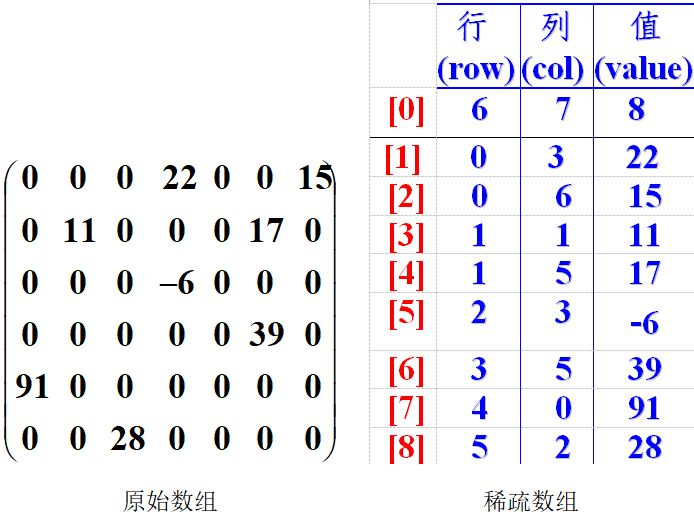
二维数组转稀疏数组
class TwoDimensionArrayDemo {
// 将二维数组转换为稀疏数组
public static int[][] twoDimensionArrayToSparseArray(int[][] array) {
// 记录棋盘中有效值的数量
int sum = 0;
int row = array.length;
int column = 0;
for (int[] ints : array) {
column = ints.length;
for (int item : ints) {
if (item != 0) {
sum++;
}
}
}
// 创建稀疏数组
int[][] sparseArray = new int[sum + 1][3];
sparseArray[0][0] = row;
sparseArray[0][1] = column;
sparseArray[0][2] = sum;
// 给稀疏数组赋值
int count = 0;
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
if (array[i][j] != 0) {
count++;
sparseArray[count][0] = i;
sparseArray[count][1] = j;
sparseArray[count][2] = array[i][j];
}
}
}
System.out.println("稀疏数组====》");
for (int i = 0; i < sparseArray.length; i++) {
System.out.printf("%d\t%d\t%d\t\n", sparseArray[i][0], sparseArray[i][1], sparseArray[i][2]);
}
return sparseArray;
}
}
稀疏数组转二维数组
class TwoDimensionArrayDemo {
// 稀疏数组转二维数组
public static int[][] sparseArrayToTwoDimensionArray(int[][] sparseArray) {
int[][] toTwoDimensionArray = new int[sparseArray[0][0]][sparseArray[0][1]];
// 给二维数组赋值
for (int i = 1; i < sparseArray.length; i++) {
toTwoDimensionArray[sparseArray[i][0]][sparseArray[i][1]] = sparseArray[i][2];
}
System.out.println("二维数组====》");
for (int[] row : toTwoDimensionArray) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
return toTwoDimensionArray;
}
}
链表
链表是一种线性数据结构,由一系列节点组成,每个节点包含数据部分和指向下一个节点的指针。根据链接方式的不同,链表分为单链表、双向链表和循环链表等。链表的特点是节点在内存中不需要连续存储,依靠指针建立逻辑关系。
链表的插入和删除操作效率较高,不需要像数组那样移动大量元素,适合频繁动态操作的场景。链表可以灵活地扩展大小,无需预定义容量,减少了内存浪费。由于节点的分散存储特性,链表更适合在内存碎片化严重时使用。
链表需要额外的指针存储空间,增加了内存开销。由于不能通过索引直接访问元素,查找操作需要遍历整个链表,效率较低。链表的指针操作较复杂,容易因指针错误引发问题,如内存泄漏或非法访问。
链表广泛应用于动态内存分配和操作频繁的场景,例如实现堆栈、队列或双端队列等数据结构。链表还被用于处理哈希冲突的链地址法和许多递归算法。在操作系统中,链表常用于管理内存块或任务队列。
单向链表
单向链表是一种链表数据结构,其中每个节点包含两部分:存储数据的部分和指向下一个节点的指针。节点按照指针的链接方向形成一个线性序列,最后一个节点的指针通常指向空(null),表示链表的结束。 单向链表适用于简单的链式结构场景,操作效率高,但只能顺序访问节点,查找效率较低。
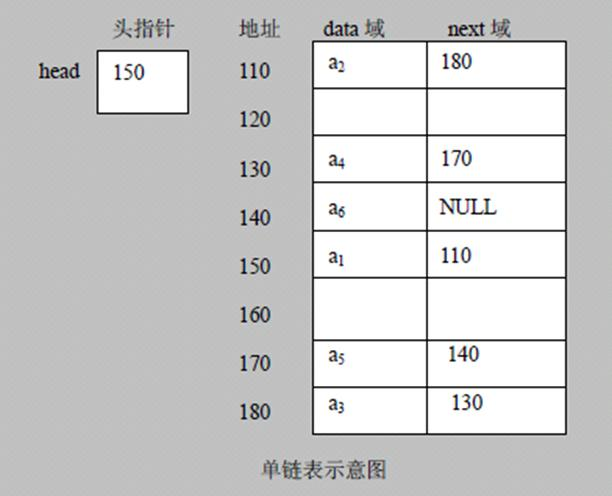
操作单向链表,对于插入、删除操作,只能定位至待操作节点的前一个节点,如果定位至当前节点,那么其上一个节点的信息便会丢失。
class SingleLinkedList{
// 头结点
private Node headNode = new Node(0,"");
// 添加方法
public void add(Node node){
Node tmpNode = headNode;
while (tmpNode.next != null){
// 指向下一个结点
tmpNode = tmpNode.next;
}
// 退出循环意味着tmpNode.next == null 即找到最后一个结点了
tmpNode.next = node;
}
// 顺序添加
public void addByOrder(Node node){
boolean flag = false;
Node tmp = headNode;
while (true){
if (tmp.next == null) {
break;
}
// 将新插入的结点num跟链表中已经存在的num进行比较,如果 < 链表中的结点 则说明找到了该位置
if (node.num < tmp.next.num){
break;
}
// 如果num相同则不能添加
if (node.num == tmp.next.num){
flag = true;
break;
}
tmp = tmp.next;
}
if (!flag){
node.next = tmp.next;
tmp.next = node;
return;
}
System.out.printf("需要添加的结点编号:%d已经存在了",node.num);
}
// 遍历链表
public void list() {
// 遍历除了头结点外的所有结点
Node tmpNode = headNode.next;
if (tmpNode == null){
System.out.println("链表为空!");
return;
}
while (tmpNode != null){
System.out.println(tmpNode);
// 指向下一个结点
tmpNode = tmpNode.next;
}
}
}
class Node {
int num;
String name;
Node next;
public Node(int num,String name){
this.num = num;
this.name = name;
}
@Override
public String toString() {
return "Node{" +
"num=" + num +
", name='" + name + '\'' +
'}';
}
}
反转单向链表
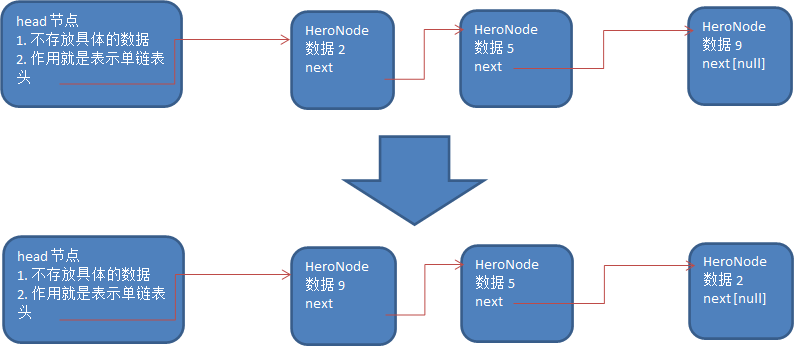
class LinkedListDemo{
// 反转链表
public void reserve(Node head) {
if (head.next == null || head.next.next == null) {
return;
}
Node reserve = new Node(0, "");
Node cur = head.next;
Node next = null;
// 遍历链表
// 遍历原来的链表,每遍历一个节点,就将其取出,并放在新的链表reverseHead 的最前端
while (cur != null) {
// 保存当前结点的下一个结点
next = cur.next;
// 将cur的下一个节点指向新的链表的最前端(覆盖掉)保证将最新的结点放到reseve的最前面
cur.next = reserve.next;
// 将cur 连接到新的链表上
reserve.next = cur;
// 将之前保存好的结点赋值给当前结点
cur = next;
}
}
}
利用栈逆序打印单向链表
class LinkedListDemo {
public void reservePrint(Node head) {
if (head.next == null || head.next.next == null) {
return;
}
Stack<Node> nodes = new Stack<>();
Node tmp = head.next;
while (tmp != null) {
nodes.push(tmp);
tmp = tmp.next;
}
// 从stack中取出结点
while (nodes.size() > 0) {
System.out.println(nodes.pop());
}
}
}
双向链表
双向链表是一种链表结构,每个节点包含三个部分:存储数据的部分、指向前一个节点的指针、指向下一个节点的指针。通过前后指针,双向链表可以在两个方向上遍历节点。
节点可以从头到尾或从尾到头进行访问,操作更加灵活。插入和删除操作比单向链表更高效,无需从头遍历即可调整指针。但每个节点存储两个指针,增加了内存开销。
单向链表,查找的方向只能是一个方向,而双向链表可以向前或者向后查找;单向链表不能自我删除,需要靠辅助节点,而双向链表,则可以自我删除。
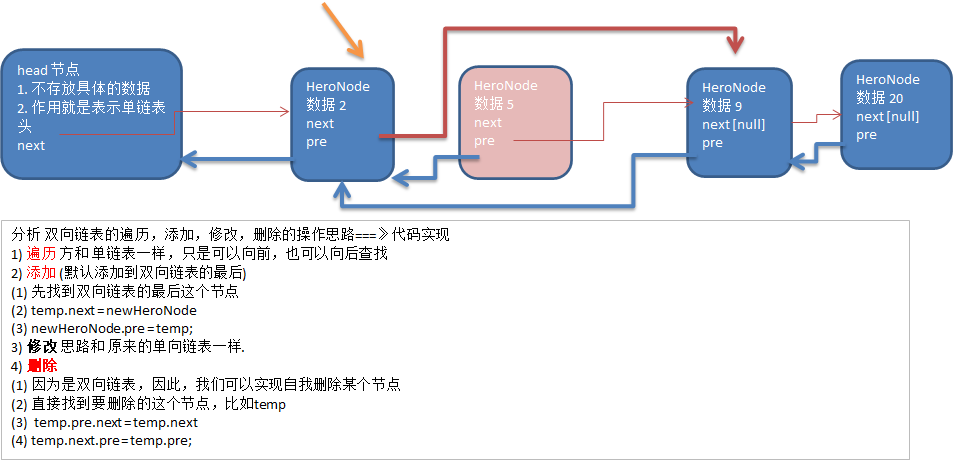
双向链表适用于需要频繁插入、删除,以及需要双向遍历的场景,例如实现双端队列或LRU缓存。
class DoubleLinkedList{
// 头结点
private Node headNode = new Node(0,"");
public Node getHeadNode() {
return headNode;
}
// 添加方法
public void add(Node node){
Node tmpNode = headNode;
while (tmpNode.next != null){
// 指向下一个结点
tmpNode = tmpNode.next;
}
// 退出循环意味着tmpNode.next == null 即找到最后一个结点了
tmpNode.next = node;
node.prev = tmpNode;
}
// 双向链表修改
public void update(Node node){
if (headNode == null) {
return;
}
Node tmp = headNode.next;
while (true){
if (tmp == null){
break;
}
if (node.num == tmp.num){
tmp.name = node.name;
break;
}
tmp = tmp.next;
}
}
// 双向链表删除
public void remove(int num){
if (headNode.next == null){
System.out.println("链表为空,无法删除!");
return;
}
Node tmp = headNode.next;
while (tmp != null){
if (num == tmp.num){
tmp.prev.next = tmp.next;
// 最后一个结点的next 为null null.pre会出现空指针异常
if(tmp.next != null) {
tmp.next.prev = tmp.prev;
}
break;
}
tmp = tmp.next;
}
}
// 遍历链表
public void list() {
// 遍历除了头结点外的所有结点
Node tmpNode = headNode.next;
if (tmpNode == null){
System.out.println("链表为空!");
return;
}
while (tmpNode != null){
System.out.println(tmpNode);
// 指向下一个结点
tmpNode = tmpNode.next;
}
}
}
class Node {
int num;
String name;
Node next;
Node prev;
public Node(int num,String name){
this.num = num;
this.name = name;
}
@Override
public String toString() {
return "Node{" +
"num=" + num +
", name='" + name + '\'' +
'}';
}
}
约瑟夫问题
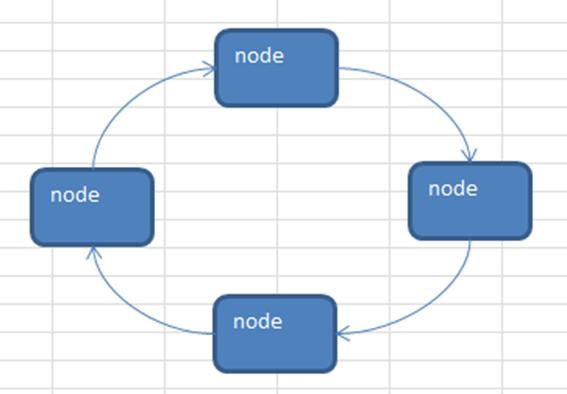
约瑟夫问题是一个经典的数学问题,描述了在环形链表中按一定规则进行删除的过程:
有 n 个人围成一圈,从第一个人开始报数,每报到第 m 个时,此人出列,接着从下一个人开始报数,重复这一过程直到圈中只剩下最后一个人。
用一个不带头结点的循环链表来处理约瑟夫问题:先构成一个有 n 个结点的单循环链表,然后由 k 结点起从 1 开始计数,计到 m 时,对应结点从链表中删除,然后再从被删除结点的下一个结点又从 1 开始计数,直到最后一个结点从链表中删除算法结束。
class JoesphSingletonLinkedList {
private Node first = null;
// 向单向链表添加数据
public void add(int nums) {
if (nums < 1) {
System.out.println("nums的值不正确");
return;
}
Node cur = null;
for (int i = 1; i <= nums; i++) {
Node node = new Node(i);
if (i == 1) {
first = node;
first.next = first;
cur = first;
} else {
cur.next = node;
node.next = first;
cur = node;
}
}
}
// 遍历单向循环链表
public void list() {
Node tmp = first;
while (true){
System.out.printf("当前结点为:%d\n",tmp.num);
if (tmp.next == first){
break;
}
tmp = tmp.next;
}
}
// 约瑟夫问题
public void joseph(int startNum,int countNum,int sum){
if (startNum > sum || startNum < 0 || countNum < 0) {
System.out.println("输入的参数不正确!");
return;
}
// 创建辅助指针,将该指针指向 first 的前一个
Node helper = first;
while (helper.next != first) {
helper = helper.next;
}
// 将first 和 help指针循环 (startNum - 1)次;因为从startNum开始,需要减一
for (int i = 0; i < startNum - 1; i++) {
first = first.next;
helper = helper.next;
}
while (true){
// 当环形链表中只存在一个结点
if (first == helper){
break;
}
// 因为是环形链表,所以需要循环挨个出链表
for (int i = 0; i < countNum - 1; i++) {
first = first.next;
helper = helper.next;
}
// 当前 first 就是出圈的结点
System.out.printf("当前出队列的结点编号为:%d\n",first.num);
first = first.next;
helper.next = first;
}
System.out.printf("最后的结点为:%d\n",first.num);
}
}
class Node {
int num;
Node next;
public Node(int num){
this.num = num;
}
@Override
public String toString() {
return "Node{" +
"num=" + num +
'}';
}
}
栈
栈是一种线性数据结构,具有后进先出(LIFO, Last In First Out)的特性。元素只能在栈顶进行插入(入栈)和删除(出栈),栈底固定不变。常用的栈实现方式包括顺序栈(使用数组)和链式栈(使用链表)。
栈操作简单,只需在栈顶执行入栈和出栈操作,效率较高,适合处理后进先出的任务。顺序栈内存连续,访问速度快,链式栈动态分配内存,空间利用率高。
但是栈容量有限,顺序栈可能出现栈溢出问题,链式栈需要额外存储指针增加内存开销。由于只能操作栈顶,无法直接访问其他元素,灵活性较低。
栈常用于程序调用栈来管理函数调用和返回,表达式求值(如中缀转后缀表达式)以及深度优先搜索(DFS)。浏览器的前进后退功能也依赖于栈结构。
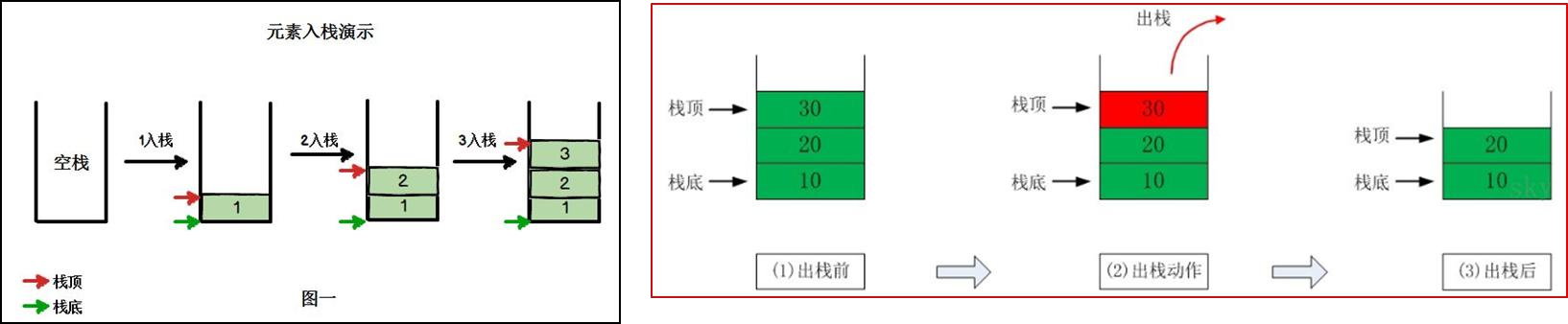
下图是出栈和入栈
数组模拟栈
class ArrayStack<T>{
private int size;
private int top;
private Object[] stack;
public ArrayStack(int size) {
this.size = size;
this.stack = new String[size];
top = -1;
}
public boolean isFull(){
return top == size -1;
}
public boolean isEmpty() {
return top == -1;
}
// 入栈
public void push(T item) {
if (isFull()) {
System.out.println("栈已经满了,不能继续添加!");
return;
}
top++;
this.stack[top] = item;
}
// 出栈操作
public T pop() {
if (isEmpty()) {
throw new RuntimeException("栈已经为空,不能继续pop");
}
T val = (T)this.stack[top];
top--;
return val;
}
// 遍历栈
public void list() {
if (isEmpty()) {
System.out.println("栈为空不能继续遍历!");
return;
}
System.out.println("遍历栈==》");
for (int i = top; i >=0; i--){
System.out.println(this.stack[i]);
}
}
}
栈实现中缀表达式
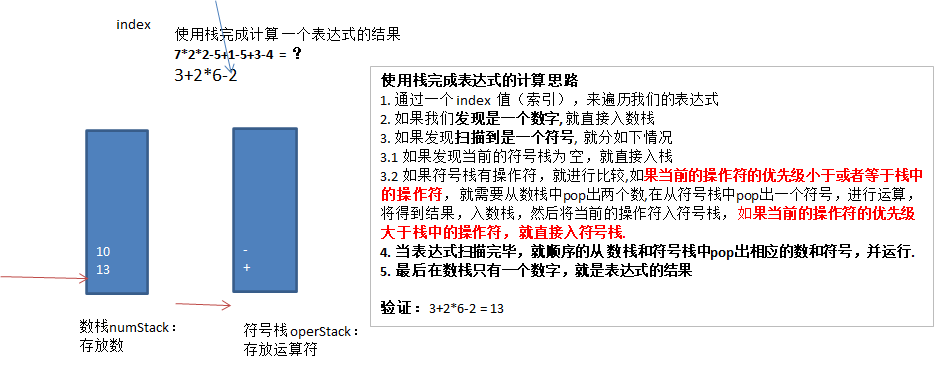
中缀表达式是一种数学表达式的表示形式,其中运算符位于操作数之间。这是人类书写和理解数学表达式最常用的格式,例如 A + B 或 3 * (4 + 5)。中缀表达式需要根据运算符优先级和括号的规则确定运算顺序。
class CalcInfixExpressions {
public int calcInfixExpressions(String expression) {
// 定义变量
char[] chars = expression.toCharArray();
int len = chars.length;
Stack<Integer> numStack = new Stack<>();
Stack<Character> oprStack = new Stack<>();
int index = 0;
for (int j = 0; j < len; j++) {
char ch = chars[j];
index++;
// 判断字符是否为数字,如果是数字就放入数栈中
if (Character.isDigit(ch)) {
// 接收多位数
int num = ch;
boolean flag = false;
// 从当前字符开始遍历,如果下一位字符不是数字,则将该数字压入栈中并退出循环,如果是数字,则需要拼接起来
for (int i = index; i < len; i++) {
if (Character.isDigit(expression.charAt(i))) {
String strNum = String.valueOf(ch) + expression.charAt(i);
num = Integer.parseInt(strNum);
flag = true;
index++;
j++;
}else {
break;
}
}
if (!flag) {
num -= 48;
}
numStack.push(num);
continue;
}
// 非数字,即运算符,如果为空直接加入栈中
if (oprStack.isEmpty()) {
oprStack.push(ch);
continue;
}
// 如果运算符栈不为空,需要比较运算符的优先级,如果当前运算符的优先级 <= 栈顶的运算符的优先级,需要计算在压入栈中
if (oprPriority(oprStack.peek()) >= oprPriority(ch)) {
numStack.push(calc(numStack.pop(), numStack.pop(), oprStack.pop()));
}
// 将字符压入操作符栈中
oprStack.push(ch);
}
// 将处理好的数据按照顺序弹出,进行计算,得到数栈中最后一个数就是最终的结果
while (!oprStack.isEmpty()){
numStack.push(calc(numStack.pop(), numStack.pop(), oprStack.pop()));
}
return numStack.pop();
}
// 获取字符的优先级
private int oprPriority(int ch) {
if (ch == '*' || ch == '/') {
return 2;
}
if (ch == '+' || ch == '-') {
return 1;
}
return -1;
}
// 计算
private int calc(int num1, int num2, int opr) {
int res = 0;
switch (opr) {
case '+':
res = num1 + num2;
break;
case '-':
res = num2 - num1;
break;
case '*':
res = num1 * num2;
break;
case '/':
res = num2 / num1;
break;
}
return res;
}
}
栈实现后缀表达式
后缀表达式又称逆波兰表达式,与前缀表达式相似,只是运算符位于操作数之后。例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 –
后缀表达式广泛应用于计算器和编译器中,因其无需运算符优先级和括号即可直接求值,适合用于表达式计算的实现。计算器通过将中缀表达式转换为后缀表达式来高效求值,避免优先级判断的复杂性。编译器在代码生成过程中使用后缀表达式来表示操作顺序,便于生成更高效的机器指令。后缀表达式还常见于数学工具和嵌入式设备中,因其解析简单且执行效率高,适合资源受限的场景。
实现思路,从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果。
class PolandNotation{
// 计算后缀表达式
public int calcSuffixExceptions(String suffixExpres) {
char[] chars = suffixExpres.toCharArray();
Stack<Integer> stack = new Stack<>();
int res =0;
for (int i = 0; i < chars.length; i++) {
char ch = suffixExpres.charAt(i);
if (!Character.isDigit(ch)) {
res = calc(stack.pop(),stack.pop(),ch);
stack.push(res);
}else {
stack.push(ch - 48);
}
}
return res;
}
// 计算
private int calc(int num1, int num2, int opr) {
int res = 0;
switch (opr) {
case '+':
res = num1 + num2;
break;
case '-':
res = num2 - num1;
break;
case '*':
res = num1 * num2;
break;
case '/':
res = num2 / num1;
break;
default:
throw new RuntimeException("运算符有误");
}
return res;
}
}
中缀表达式转后缀表达式
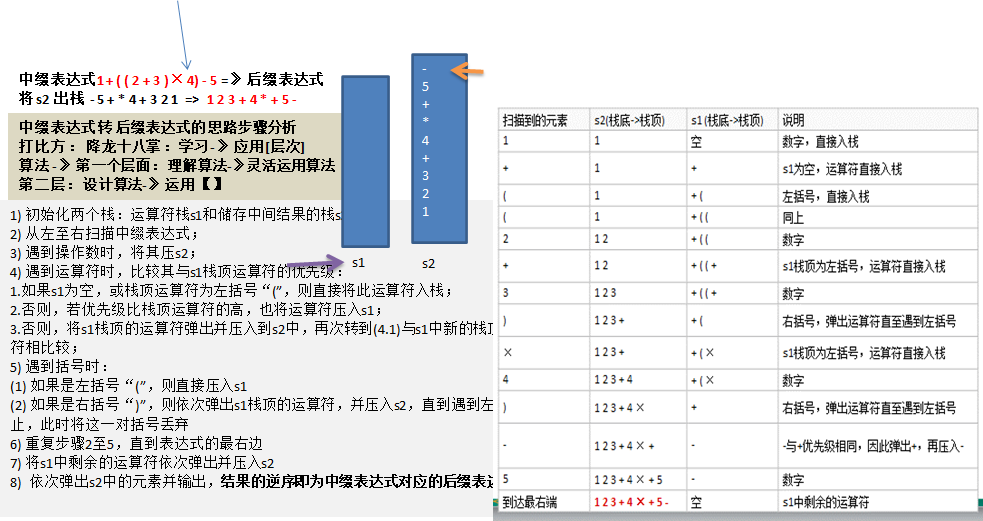
中缀表达式转后缀表达式代码实现
class InfixToPolandNotation{
// 根据ASCII 判断是否为数字
private boolean isNumber(char ch){
return ch >=48 && ch <= 57;
}
// 获取字符的优先级
private int oprPriority(String opr) {
if (opr.equals("*") || opr.equals("/")) {
return 2;
}
if (opr.equals("+") || opr.equals("-")) {
return 2;
}
return -1;
}
// 将中缀表达式字符串转成中缀表达式集合
public List<String> toInfixExceptionList(String str) {
ArrayList<String> list = new ArrayList<>();
int index = 0;
StringBuilder number;
char c;
while (index < str.length()){
if (!isNumber((c = str.charAt(index)))){
list.add(String.valueOf(c));
index++;
}else {
number = new StringBuilder();
while (index < str.length() && isNumber((c = str.charAt(index)))){
index++;
number.append(c);
}
list.add(number.toString());
}
}
return list;
}
// 将中缀表达式转为后缀表达式
public List<String> infixExpressionToSuffixExpress(List<String> list) {
Stack<String> stack = new Stack<>();
ArrayList<String> finalList = new ArrayList<>();
for (String item : list) {
// 如果是数字或者为( 将该值压入栈中
if (item.matches("\\d+")){
finalList.add(item);
continue;
}
if (item.equals("(")){
stack.push(item);
continue;
}
// 如果是 )则将 ()中间的数重新压入list中,最后将 ) 移除掉
if (item.equals(")")){
while (!stack.peek().equals("(")) {
finalList.add(stack.pop());
}
stack.pop();
}else {
// 如果不是 )则判断运算符的优先级,如果符号栈栈顶的优先级 >= 当前的优先级,则将该运算符加入数字栈中
while (stack.size() > 0 && oprPriority(stack.peek()) >= oprPriority(item)){
finalList.add(stack.pop());
}
stack.push(item);
}
}
// 将operStack中剩余的运算符依次弹出并加入tempList
while (stack.size() != 0) {
finalList.add(stack.pop());
}
return finalList;
}
}
完整逆波兰表达式代码,支持小数、支持消除空格
public class ReversePolishMultiCalc {
/**
* 匹配 + - * / ( ) 运算符
*/
static final String SYMBOL = "\\+|-|\\*|/|\\(|\\)";
static final String LEFT = "(";
static final String RIGHT = ")";
static final String ADD = "+";
static final String MINUS= "-";
static final String TIMES = "*";
static final String DIVISION = "/";
/**
* 加減 + -
*/
static final int LEVEL_01 = 1;
/**
* 乘除 * /
*/
static final int LEVEL_02 = 2;
/**
* 括号
*/
static final int LEVEL_HIGH = Integer.MAX_VALUE;
static Stack<String> stack = new Stack<>();
static List<String> data = Collections.synchronizedList(new ArrayList<String>());
/**
* 去除所有空白符
* @param s
* @return
*/
public static String replaceAllBlank(String s ){
// \\s+ 匹配任何空白字符,包括空格、制表符、换页符等等, 等价于[ \f\n\r\t\v]
return s.replaceAll("\\s+","");
}
/**
* 判断是不是数字 int double long float
* @param s
* @return
*/
public static boolean isNumber(String s){
Pattern pattern = Pattern.compile("^[-\\+]?[.\\d]*$");
return pattern.matcher(s).matches();
}
/**
* 判断是不是运算符
* @param s
* @return
*/
public static boolean isSymbol(String s){
return s.matches(SYMBOL);
}
/**
* 匹配运算等级
* @param s
* @return
*/
public static int calcLevel(String s){
if("+".equals(s) || "-".equals(s)){
return LEVEL_01;
} else if("*".equals(s) || "/".equals(s)){
return LEVEL_02;
}
return LEVEL_HIGH;
}
/**
* 匹配
* @param s
*/
public static List<String> doMatch (String s) throws Exception{
if(s == null || "".equals(s.trim())) throw new RuntimeException("data is empty");
if(!isNumber(s.charAt(0)+"")) throw new RuntimeException("data illeagle,start not with a number");
s = replaceAllBlank(s);
String each;
int start = 0;
for (int i = 0; i < s.length(); i++) {
if(isSymbol(s.charAt(i)+"")){
each = s.charAt(i)+"";
//栈为空,(操作符,或者 操作符优先级大于栈顶优先级 && 操作符优先级不是( )的优先级 及是 ) 不能直接入栈
if(stack.isEmpty() || LEFT.equals(each)
|| ((calcLevel(each) > calcLevel(stack.peek())) && calcLevel(each) < LEVEL_HIGH)){
stack.push(each);
}else if( !stack.isEmpty() && calcLevel(each) <= calcLevel(stack.peek())){
//栈非空,操作符优先级小于等于栈顶优先级时出栈入列,直到栈为空,或者遇到了(,最后操作符入栈
while (!stack.isEmpty() && calcLevel(each) <= calcLevel(stack.peek()) ){
if(calcLevel(stack.peek()) == LEVEL_HIGH){
break;
}
data.add(stack.pop());
}
stack.push(each);
}else if(RIGHT.equals(each)){
// ) 操作符,依次出栈入列直到空栈或者遇到了第一个)操作符,此时)出栈
while (!stack.isEmpty() && LEVEL_HIGH >= calcLevel(stack.peek())){
if(LEVEL_HIGH == calcLevel(stack.peek())){
stack.pop();
break;
}
data.add(stack.pop());
}
}
start = i ; //前一个运算符的位置
}else if( i == s.length()-1 || isSymbol(s.charAt(i+1)+"") ){
each = start == 0 ? s.substring(start,i+1) : s.substring(start+1,i+1);
if(isNumber(each)) {
data.add(each);
continue;
}
throw new RuntimeException("data not match number");
}
}
//如果栈里还有元素,此时元素需要依次出栈入列,可以想象栈里剩下栈顶为/,栈底为+,应该依次出栈入列,可以直接翻转整个stack 添加到队列
Collections.reverse(stack);
data.addAll(new ArrayList<>(stack));
System.out.println(data);
return data;
}
/**
* 算出结果
* @param list
* @return
*/
public static Double doCalc(List<String> list){
Double d = 0d;
if(list == null || list.isEmpty()){
return null;
}
if (list.size() == 1){
System.out.println(list);
d = Double.valueOf(list.get(0));
return d;
}
ArrayList<String> list1 = new ArrayList<>();
for (int i = 0; i < list.size(); i++) {
list1.add(list.get(i));
if(isSymbol(list.get(i))){
Double d1 = doTheMath(list.get(i - 2), list.get(i - 1), list.get(i));
list1.remove(i);
list1.remove(i-1);
list1.set(i-2,d1+"");
list1.addAll(list.subList(i+1,list.size()));
break;
}
}
doCalc(list1);
return d;
}
/**
* 运算
* @param s1
* @param s2
* @param symbol
* @return
*/
public static Double doTheMath(String s1,String s2,String symbol){
Double result ;
switch (symbol){
case ADD : result = Double.valueOf(s1) + Double.valueOf(s2); break;
case MINUS : result = Double.valueOf(s1) - Double.valueOf(s2); break;
case TIMES : result = Double.valueOf(s1) * Double.valueOf(s2); break;
case DIVISION : result = Double.valueOf(s1) / Double.valueOf(s2); break;
default : result = null;
}
return result;
}
public static void main(String[] args) {
//String math = "9+(3-1)*3+10/2";
String math = "12.8 + (2 - 3.55)*4+10/5.0";
try {
doCalc(doMatch(math));
} catch (Exception e) {
e.printStackTrace();
}
}
}
队列
队列是一种先进先出的线性数据结构,可以使用数组或链表来实现。它允许从一端(队尾)添加元素,从另一端(队头)移除元素。队列的操作包括入队和出队,遵循先入先出的原则。即先存入队列的数据,要先取出,后存入的要后取出。
队列结构简单,便于实现顺序管理,适用于按序处理任务的场景。在并发环境中,队列可以用来缓冲任务,起到流量控制的作用。由于其先进先出的特性,队列能够保证数据处理的公平性,避免任务乱序。
队列有固定的操作顺序,灵活性较低,无法直接访问中间的元素。在存储空间不足或队列已满的情况下,可能需要动态调整大小或处理溢出问题。在多线程环境中,队列需要额外的同步机制,可能影响性能。
队列广泛应用于任务调度和资源分配,例如打印队列、操作系统中的进程调度等。它在数据传输中被用作缓冲区,例如消息队列用于异步通信。队列还常用于广度优先搜索(BFS)等算法中,用来管理节点的访问顺序。
使用数组模拟队列示意图:
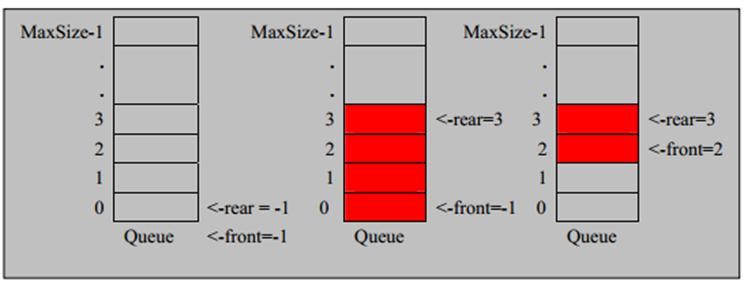
数组模拟单向队列
public class ArrayQueue{
// 队列容量
private int capacity;
// 保存队列中的数据
private int[] arr;
// 头部指针
private int front;
// 尾部指针
private int rear;
public ArrayQueue(int capacity) {
this.capacity = capacity;
arr = new int[capacity];
front = -1;
rear = -1;
}
public boolean isEmpty() {
return front == rear;
}
public boolean isFull() {
return capacity - 1 == rear;
}
public void add(int data) {
if (isFull()) {
System.out.println("队列已经满了,不能在继续添加");
return;
}
arr[++rear] = data;
}
public int get() {
if (isEmpty()) {
System.out.println("队列为空,不能获取元素");
return -1;
}
return arr[++front];
}
// 显示队列的所有数据
public void show() {
if (isEmpty()) {
System.out.println("队列空的,没有数据~~");
return;
}
System.out.println("开始遍历队列:");
for (int i = front + 1; i <= rear; i++) {
System.out.printf("arr[%d]=%d\n", i, arr[i]);
}
}
// 显示队列的头数据, 注意不是取出数据
public int peek() {
if (isEmpty()) {
throw new RuntimeException("队列空的,没有数据~~");
}
return arr[front + 1];
}
}
数组模拟环形队列
public class CircleArrayQueue{
// 队列容量
private int capacity;
// 保存队列中的数据
private int[] arr;
// 头部指针
private int front;
// 尾部指针
private int rear;
public CircleArrayQueue(int capacity) {
this.capacity = capacity;
arr = new int[capacity];
}
public boolean isEmpty() {
return front == rear;
}
public boolean isFull() {
// 此处+1 是因为存储元素从0算起
return (rear + 1) % capacity == front;
}
public void add(int data) {
if (isFull()) {
System.out.println("队列已经满了,不能在继续添加");
return;
}
arr[rear] = data;
rear = (rear + 1) % capacity;
}
public int get() {
if (isEmpty()) {
System.out.println("队列为空,不能获取元素");
return -1;
}
int value = arr[front];
front = (front + 1) % capacity;
return value;
}
// 显示队列的所有数据
public void show() {
if (isEmpty()) {
System.out.println("队列空的,没有数据~~");
return;
}
System.out.println("开始遍历队列:");
for (int i = front % capacity; i < front + ((rear + capacity - front) % capacity); i++) {
System.out.printf("arr[%d]=%d\n", i, arr[i]);
}
}
// 显示队列的头数据, 注意不是取出数据
public int peek() {
if (isEmpty()) {
throw new RuntimeException("队列空的,没有数据~~");
}
return arr[front];
}
}
哈希表
哈希表是一种通过哈希函数将键映射到特定位置的数据结构,用于快速存储和查找键值对。它利用数组存储数据,并通过哈希函数确定每个键的存储位置,当发生冲突时通过开放地址法或链地址法解决。
哈希表能够以常数时间复杂度完成查找、插入和删除操作(理想情况下),适合处理大量数据的快速检索。与其他数据结构相比,操作效率高且实现相对简单。
哈希表需要依赖合适的哈希函数,若函数分布不均会导致大量冲突,从而降低性能。表的扩展或收缩可能导致重新哈希,增加额外开销。在需要保持数据顺序或进行区间查询时不适用。
哈希表适用于需要高效查找的场景,例如字典、缓存系统、数据库索引、计数统计以及散列密码存储。它常被用于实现集合、映射等数据结构。
代码模拟哈希表
public class HashTableDemo {
public static void main(String[] args) {
HashTab hashTab = new HashTab(3);
Node node1 = new Node(1, "zs");
Node node2 = new Node(2, "lx");
Node node3 = new Node(3, "ex");
Node node4 = new Node(4, "as");
Node node5 = new Node(7, "we");
hashTab.put(node1);
hashTab.put(node2);
hashTab.put(node3);
hashTab.put(node4);
hashTab.put(node5);
System.out.println("添加元素后===》");
System.out.println(hashTab.toString());
System.out.println("删除后===》");
hashTab.remove(4);
System.out.println(hashTab.toString());
}
}
class HashTab {
private NodeList[] nodes;
private int size;
public HashTab(int size) {
this.size = size;
nodes = new NodeList[size];
for (int i = 0; i < size; i++) {
nodes[i] = new NodeList();
}
}
public void put(Node node) {
// 放入hash表的位置
nodes[getPosition(node.id)].add(node);
}
public void remove(int id) {
nodes[getPosition(id)].delete(id);
}
private int getPosition(int id) {
return id % size;
}
@Override
public String toString() {
return "HashTab{" +
"nodes=\n" + Arrays.toString(nodes) +
"}";
}
}
class NodeList {
// 头结点
Node head = null;
// 添加结点方法
public void add(Node node) {
if (head == null) {
head = node;
return;
}
// 头结点不要动,将添加的结点放到链表的最后一个位置
Node tmp = head;
// 当下一个结点等于null时,找到最后一个结点
while (tmp.next != null) {
tmp = tmp.next;
}
tmp.next = node;
}
// 展示当前链表
public void list() {
if (head == null) {
System.out.println("当前链表为空");
return;
}
// 辅助结点
Node tmp = head;
while (true) {
System.out.println(tmp);
if (tmp.next == null) {
break;
}
tmp = tmp.next;
}
}
// 根据ID删除链表中的某个结点
public void delete(int id) {
if (head == null) {
System.out.println("当前链表为空");
return;
}
// 判断删除的是否是头结点
if (head.id == id) {
head = head.next;
return;
}
Node preNode = head;
Node curNode = preNode.next;
while (curNode != null) {
if (curNode.id == id) {
preNode.next = curNode.next;
System.out.println("删除成功,删除的是: " + curNode.id + "," + curNode.name);
curNode = null;
return;
}
preNode = preNode.next;
curNode = curNode.next;
}
System.out.println("删除失败,节点不存在");
}
@Override
public String toString() {
return "NodeList{" +
"head=" + head +
"}\n";
}
}
class Node {
int id;
String name;
Node next;
public Node(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "Node{" +
"id=" + id +
", name='" + name + '\'' +
", next=" + next +
"}";
}
}
非线性数据结构
非线性数据结构是指数据元素之间没有直接的顺序关系。与线性数据结构相比,非线性数据结构中的元素可以通过多种方式连接。常见的非线性数据结构包括树和图。树是一种分层结构,每个节点可以有多个子节点,常用于表示层次关系,如文件系统。图则是由节点和边组成,适用于表示复杂的关系,如社交网络和网络拓扑。
| 数据结构 | 特点 | 优点 | 缺点 | 使用场景 |
|---|---|---|---|---|
| 树 | 节点具有层次结构,每个节点可以有多个子节点 | 表达层次关系清晰,便于查找和组织数据 | 结构复杂,操作较为复杂 | 文件系统、目录结构、数据库索引等 |
| 图 | 由节点和边组成,可以表示任意关系 | 能够表达复杂的关系,灵活性高 | 存储和操作复杂,需要额外的空间和时间 | 社交网络、网络路由、推荐系统等 |
二叉树
二叉树是一种树形数据结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树可以是空树,也可以由一个根节点及其左右子树组成,通过递归定义实现。
二叉树结构简单且容易实现,可以通过不同的遍历方式(前序、中序、后序)高效访问节点。在特定场景下(如平衡二叉树或二叉搜索树),可以实现高效的查找、插入和删除操作。 普通二叉树可能因结构不平衡导致操作效率下降,最坏情况下退化为链表。维护平衡的二叉树(如 AVL 树或红黑树)需要额外的时间和空间开销。
二叉树常用于表达式解析(如构建语法树)、快速查找(如二叉搜索树)、优先级管理(如堆结构)、文件压缩(如哈夫曼树),以及解决图形渲染和路径规划等问题。
二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个结点。
如果该二叉树的所有叶子节点都在最后一层,并且结点总数为2^n -1,n 为层数,则称为满二叉树。
如果该二叉树的所有叶子节点都在最后一层或者倒数第二层,而且最后一层的叶子节点在左边连续,倒数第二层的叶子节点在右边连续,我们称为完全二叉树。
二叉树的遍历及查找
对于二叉树来讲最主要、最基本的运算是遍历。遍历二叉树 是指以一定的次序访问二叉树中的每个结点。所谓访问结点是指对结点进行各种操作的简称。
例如,查询结点数据域的内容,或输出它的值,或找出结点位置,或是执行对结点的其他操作。遍历二叉树的过程实质是把二叉树的结点进行线性排列的过程。
二叉树的遍历方法:
- 前序遍历:先访问根结点,然后前序遍历左子树,在前序遍历右子树;
- 中序遍历:中序遍历根结点的左子树,然后访问根结点,最后遍历右子树;
- 后序遍历:后序遍历左子树,然后后序遍历右子树,最后访问根结点;
public class BinaryTreeDemo {
public static void main(String[] args) {
BinaryTreeObj root = new BinaryTreeObj(1,"zs");
BinaryTreeObj binaryTreeObj2 = new BinaryTreeObj(2,"ls");
BinaryTreeObj binaryTreeObj3 = new BinaryTreeObj(3,"ww");
BinaryTreeObj binaryTreeObj4 = new BinaryTreeObj(4,"zq");
BinaryTreeObj binaryTreeObj5 = new BinaryTreeObj(5,"111");
root.setLeft(binaryTreeObj2);
root.setRight(binaryTreeObj3);
binaryTreeObj3.setLeft(binaryTreeObj4);
binaryTreeObj3.setRight(binaryTreeObj5);
BinaryTree binaryTree = new BinaryTree();
binaryTree.setRoot(root);
binaryTree.preOrderShow();
BinaryTreeObj binaryTreeObj = binaryTree.preOrderSearch(11);
if (binaryTreeObj == null) {
System.out.println("没有找到该结点~");
return;
}
System.out.printf("找到当前结点:id: %d, name: %s",binaryTreeObj.getId(),binaryTreeObj.getName());
}
}
class BinaryTree {
private BinaryTreeObj root;
public void setRoot(BinaryTreeObj root) {
this.root = root;
}
public void preOrderShow() {
if (this.root != null) {
this.root.preOrder();
}
}
public void postOrderShow() {
if (this.root != null) {
this.root.postOrder();
}
}
public void midOrderShow() {
if (this.root != null) {
this.root.midOrder();
}
}
public BinaryTreeObj preOrderSearch(int id){
if (this.root != null) {
return this.root.preOrderSearch(id);
}
return null;
}
public BinaryTreeObj infixOrderSearch(int id){
if (this.root != null) {
return this.root.infixOrderSearch(id);
}
return null;
}
public BinaryTreeObj postOrderSearch(int id){
if (this.root != null) {
return this.root.postOrderSearch(id);
}
return null;
}
}
class BinaryTreeObj {
private Integer id;
private String name;
public BinaryTreeObj(Integer id,String name){
this.id = id;
this.name = name;
}
public String getName() {
return name;
}
public Integer getId() {
return id;
}
private BinaryTreeObj left;
private BinaryTreeObj right;
public void setLeft(BinaryTreeObj left) {
this.left = left;
}
public void setRight(BinaryTreeObj right) {
this.right = right;
}
// 前序遍历:根结点 =》 左结点 =》 右结点
public void preOrder(){
System.out.println(this);
if (this.left != null){
this.left.preOrder();
}
if (this.right != null){
this.right.preOrder();
}
}
// 后序遍历: 左结点 =》 右结点 =》 根结点
public void postOrder(){
if (this.left != null){
this.left.postOrder();
}
if (this.right != null){
this.right.postOrder();
}
System.out.println(this);
}
// 中序遍历: 左结点 =》 根结点 =》 右结点
public void midOrder(){
if (this.left != null){
this.left.midOrder();
}
System.out.println(this);
if (this.right != null){
this.right.midOrder();
}
}
// 前序查找
public BinaryTreeObj preOrderSearch(int id) {
if (id == this.id){
return this;
}
BinaryTreeObj binaryTreeObj = null;
if (this.left != null){
binaryTreeObj = this.left.preOrderSearch(id);
}
if (binaryTreeObj != null){
return binaryTreeObj;
}
if (this.right != null){
binaryTreeObj = this.right.preOrderSearch(id);
}
return binaryTreeObj;
}
// 中序查找
public BinaryTreeObj infixOrderSearch(int id) {
BinaryTreeObj binaryTreeObj = null;
if (this.left != null){
binaryTreeObj = this.left.infixOrderSearch(id);
}
if (id == this.id){
return this;
}
if (binaryTreeObj != null){
return binaryTreeObj;
}
if (this.right != null){
binaryTreeObj = this.right.infixOrderSearch(id);
}
return binaryTreeObj;
}
// 后序查找
public BinaryTreeObj postOrderSearch(int id) {
BinaryTreeObj binaryTreeObj = null;
if (this.left != null){
binaryTreeObj = this.left.postOrderSearch(id);
}
if (binaryTreeObj != null){
return binaryTreeObj;
}
if (this.right != null){
binaryTreeObj = this.right.postOrderSearch(id);
}
if (id == this.id){
return this;
}
return binaryTreeObj;
}
@Override
public String toString() {
return "BinaryTreeObj{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
}
二叉树的删除
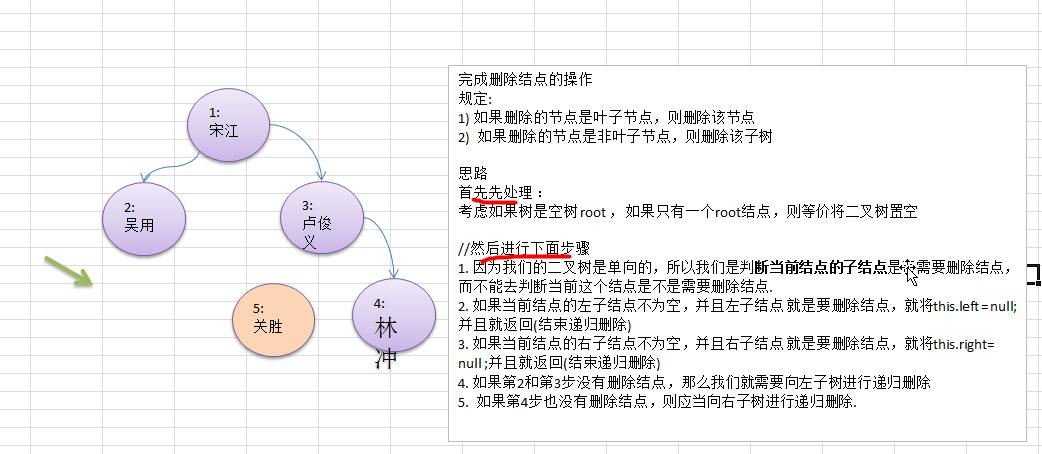
class BinaryTree {
public void del(int id){
if (this.root == null){
return;
}
if (this.root.getId() == id){
this.root = null;
return;
}
this.root.delNo(id);
}
}
class BinaryTreeObj {
// 根据ID删除结点
public void delNo(int id){
// 找到当前结点的左子树结点是否为指定结点,如果是则将其置空
if (this.left != null && this.left.id == id){
this.left = null;
return;
}
// 与上面同理删除右子树结点
if (this.right != null && this.right.id == id){
this.right = null;
return;
}
if (this.left == null && this.right == null){
return;
}
// 如果当前左结点或右结点 不是要删除的结点 则进行递归删除
if (this.left != null){
this.left.delNo(id);
}
if (this.right != null) {
this.right.delNo(id);
}
}
}
顺序存储二叉树
二叉树的顺序存储,指的是使用顺序表(数组)存储二叉树。
需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。
顺序存储二叉树应用实例:八大排序算法中的堆排序,就会使用到顺序存储二叉树。
public class ArrBinaryTreeDemo {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7};
ArrBinaryTree arrBinaryTree = new ArrBinaryTree();
arrBinaryTree.setArrayTree(arr);
arrBinaryTree.preArrBinaryTree(0);
}
}
class ArrBinaryTree {
private int[] arr = null;
public void setArrayTree(int[] arr) {
this.arr = arr;
}
public void preArrBinaryTree(int index) {
if (arr == null || arr.length == 0) {
return;
}
System.out.println(arr[index]);
int nextLeftIndex = (index << 1) + 1;
int nextRightIndex = (index << 1) + 2;
if (nextLeftIndex < arr.length) {
preArrBinaryTree(nextLeftIndex);
}
if (nextRightIndex < arr.length) {
preArrBinaryTree(nextRightIndex);
}
}
}
线索化二叉树
线索化二叉树是一种对二叉树进行优化的数据结构,通过给二叉树的空指针(即左指针或右指针为空的指针)赋予线索,使得在遍历时不需要使用栈或递归,能够更高效地访问节点。线索化二叉树中的“线索”是指通过空指针存储节点的前驱或后继节点,从而使得遍历变得更加高效。
根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种:
- 前序线索二叉树:在前序线索化二叉树中,空的左指针指向当前节点的前驱节点,空的右指针指向当前节点的后继节点。这种方式使得我们在进行前序遍历时,可以通过右指针访问当前节点的后继,或者通过左指针访问其前驱。前序线索化二叉树通常用于直接的前序遍历。
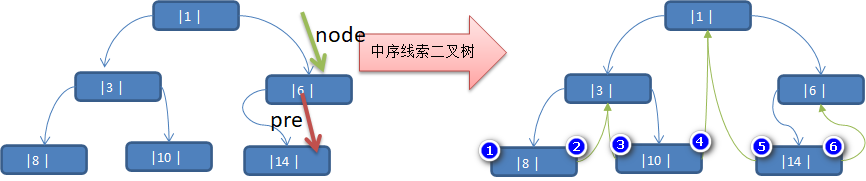
- 中序线索二叉树:中序线索化二叉树是最常见的一种类型。在这种树中,空的左指针指向当前节点的前驱节点,空的右指针指向当前节点的后继节点。由于中序遍历可以按顺序访问节点,因此这种线索化方式特别适用于需要中序遍历的情况,如二叉搜索树的遍历。
- 后序线索二叉树:在后序线索化二叉树中,空的左指针指向当前节点的前驱节点,空的右指针指向当前节点的后继节点。后序线索化二叉树的特点是可以直接通过空指针连接节点的前驱和后继,便于后序遍历。
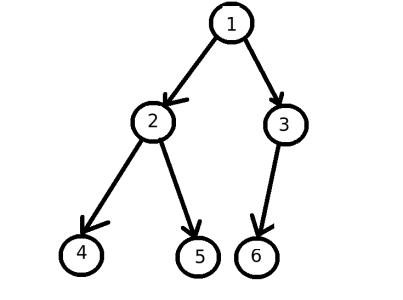
如图,按照前序遍历可以得到数组 {1, 2, 4, 5, 3, 6} 其中
- 【2】的前驱结点为【1】,后继结点为【4】
- 【6】的前驱结点为【3】,后继结点为 null
中序线索化二叉树示意图
public class ThreadedBinaryTreeDemo {
public static void main(String[] args) {
BinaryTreeObj root = new BinaryTreeObj(1,"zs");
BinaryTreeObj binaryTreeObj2 = new BinaryTreeObj(2,"ls");
BinaryTreeObj binaryTreeObj3 = new BinaryTreeObj(3,"ww");
BinaryTreeObj binaryTreeObj4 = new BinaryTreeObj(4,"zq");
BinaryTreeObj binaryTreeObj5 = new BinaryTreeObj(5,"111");
root.setLeft(binaryTreeObj2);
root.setRight(binaryTreeObj3);
binaryTreeObj3.setLeft(binaryTreeObj4);
binaryTreeObj3.setRight(binaryTreeObj5);
// 中序线索化二叉树
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.infixThreadedBinaryTree(root);
// 遍历中序线索化二叉树
threadedBinaryTree.forEachInfixThreadedBinaryTree(root); // 2,1,4,3,5
}
}
class ThreadedBinaryTree{
private BinaryTreeObj pre;
// 中序线索化二叉树
public void infixThreadedBinaryTree(BinaryTreeObj node){
if (node == null){
return;
}
// 左递归线索化二叉树
infixThreadedBinaryTree(node.getLeft());
// 线索化核心代码 将左结点线索化
if (node.getLeft() == null){
node.setLeft(pre);
node.setLeftType(1);
}
// 将右结点线索化
if (pre != null && pre.getRight() == null) {
pre.setRight(node);
pre.setRightType(1);
}
// 使辅助结点指针指向当前结点
pre = node;
// 右递归线索化二叉树
infixThreadedBinaryTree(node.getRight());
}
// 遍历中序线索二叉树
public void forEachInfixThreadedBinaryTree(BinaryTreeObj root) {
// 用辅助结点保存根结点
BinaryTreeObj node = root;
while (node != null){
// 向左子树遍历,直到找到 leftType=1 的结点,等于1代表该结点为前驱结点
while (node.getLeftType() == 0){
node = node.getLeft();
}
System.out.println(node);
// 向右子树遍历,直到找到 rightType=0 的结点, 等于0代表该结点为右子树
while (node.getRightType() == 1){
node = node.getRight();
System.out.println(node);
}
// node 结点向右边找
node = node.getRight();
}
}
}
class BinaryTreeObj {
private Integer id;
private String name;
private BinaryTreeObj left;
private BinaryTreeObj right;
// 如果leftType == 0 表示指向的是左子树, 如果 1 则表示指向前驱结点
// 如果rightType == 0 表示指向是右子树, 如果 1 表示指向后继结点
private int leftType;
private int rightType;
public BinaryTreeObj(Integer id,String name){
this.id = id;
this.name = name;
}
public String getName() {
return name;
}
public Integer getId() {
return id;
}
public BinaryTreeObj getLeft() {
return left;
}
public BinaryTreeObj getRight() {
return right;
}
public void setLeft(BinaryTreeObj left) {
this.left = left;
}
public void setRight(BinaryTreeObj right) {
this.right = right;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
public int getLeftType() {
return leftType;
}
public int getRightType() {
return rightType;
}
}
哈夫曼树
哈夫曼树是一种带权路径最短的二叉树,常用于数据压缩算法。其基本原理是根据各个字符的频率构建一颗二叉树,使得频率较高的字符具有较短的路径,频率较低的字符具有较长的路径。哈夫曼树通过贪心算法构建,常用于无损数据压缩,如文本文件的压缩。
哈夫曼树能高效地实现数据压缩,因为它根据字符出现频率动态调整树结构,使得频率较高的字符占据较短的编码,而频率较低的字符占据较长的编码,从而最大程度减少了整体编码长度。
哈夫曼树的构建和编码过程可能需要额外的时间和空间开销,尤其是在字符种类较多或者频率分布非常不均匀的情况下。对压缩后的数据进行解码时,也需要在哈夫曼树上进行逐层查找。
哈夫曼树常用于数据压缩算法(如ZIP文件格式和JPEG图像格式),以及各种无损压缩应用中。它在文本、图像、音频等需要压缩存储的场合中应用广泛,尤其在减少存储空间和提高传输效率方面发挥重要作用。
哈夫曼树重要概念:
- 路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为 1,则从根结点到第 L 层结点的路径长度为 L-1;
- 结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积;
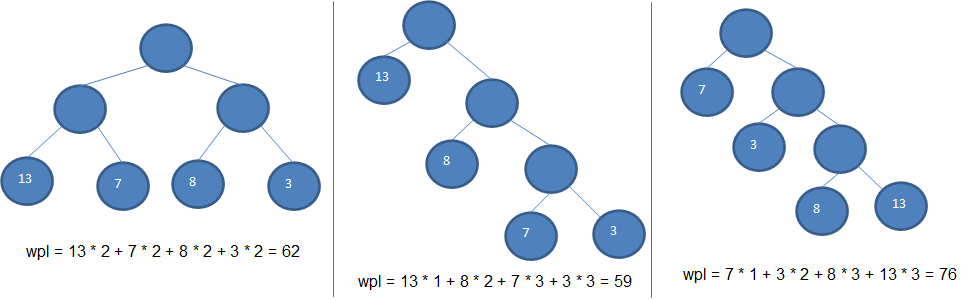
- 树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。WPL 最小的就是赫夫曼树;
给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度(WPL)达到最小,称这样的二叉树为最优二叉树,称为哈夫曼树,有些资料也译为赫夫曼树。 WPL最小的就是哈夫曼树,如图中间的树就是哈夫曼树。
public class HuffmanTreeDemo {
public static void main(String[] args) {
HuffmanTree huffmanTree = new HuffmanTree();
HuffmanTreeNode root = huffmanTree.buildHuffmanTree(new int[]{13, 7, 8, 3, 29, 6, 1});
System.out.println("前序遍历huffman树:");
huffmanTree.preOrder(root);
}
}
class HuffmanTree{
public void preOrder(HuffmanTreeNode root){
if (root != null){
root.preOrder();
}
}
public HuffmanTreeNode buildHuffmanTree(int[] arr){
List<HuffmanTreeNode> list = new ArrayList<>();
for (int value : arr) {
list.add(new HuffmanTreeNode(value));
}
// 如果集合中的元素大于1则继续循环
while (list.size() > 1){
// 从大到小进行排序
Collections.sort(list);
// 获取集合中两个较小的元素进行构建 huffman 树
HuffmanTreeNode leftNode = list.get(0);
HuffmanTreeNode rightNode = list.get(1);
HuffmanTreeNode parentNode = new HuffmanTreeNode(leftNode.value + rightNode.value);
parentNode.left = leftNode;
parentNode.right = rightNode;
// 构建后将 leftNode, rightNode 移除集合;将parentNode加入集合;然后重新排序
list.remove(leftNode);
list.remove(rightNode);
list.add(parentNode);
}
return list.get(0);
}
}
class HuffmanTreeNode implements Comparable<HuffmanTreeNode>{
int value;
HuffmanTreeNode left;
HuffmanTreeNode right;
public HuffmanTreeNode(int value){
this.value = value;
}
public void preOrder(){
System.out.println(this);
if (this.left != null){
this.left.preOrder();
}
if (this.right != null){
this.right.preOrder();
}
}
@Override
public int compareTo(HuffmanTreeNode o) {
// 从小到大排序
return this.value - o.value;
}
@Override
public String toString() {
return "HuffmanTreeNode{" +
"value=" + value +
'}';
}
}
二叉排序树
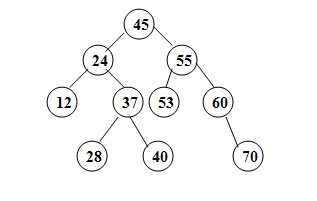
二叉排序树,也称为二叉搜索树(BST),是一种特殊的二叉树,其中每个节点都包含一个键值,并且满足以下性质:对于每个节点,其左子树中所有节点的键值都小于该节点的键值,而右子树中所有节点的键值都大于该节点的键值。这种结构使得二叉排序树在进行查找、插入和删除操作时非常高效。
二叉排序树的主要优点是它能够快速进行数据查找、插入和删除操作。在最优情况下,查找、插入和删除的时间复杂度为O(log n),这种效率对于动态数据集(数据不断变化的场景)特别有用。 如果二叉排序树的插入顺序不理想(如按升序或降序插入数据),会导致树的高度过大,退化为链表,导致查找、插入和删除操作的时间复杂度变为O(n)。这种情况下,性能大幅下降。
二叉排序树适用于需要高效动态查找的数据结构场景,特别是当数据经常更新时。它广泛应用于数据库索引、内存管理、动态集合的处理等领域。对于数据的插入和删除较为频繁的应用(如在线查询系统),二叉排序树非常有效。
class BinarySortTree {
private Node root;
public void setRoot(Node root) {
this.root = root;
}
// 添加结点
public void add(Node node) {
if (this.root == null) {
this.root = node;
} else {
this.root.add(node);
}
}
// 中序遍历
public void infixOrder() {
if (this.root != null) {
this.root.infixOrder();
}
}
// 查找结点
public Node search(int target) {
if (this.root == null) {
return null;
}
return this.root.search(target);
}
// 查找当前结点的父结点
public Node searchParentNode(int target) {
if (this.root == null) {
return null;
}
return this.root.searchParentNode(target);
}
// 删除结点
public void delNode(int target) {
if (this.root == null) {
return;
}
// 如果删除的结点是根结点
if (this.root.left == null && this.root.right == null) {
this.root = null;
return;
}
Node targetNode = search(target);
if (targetNode == null) {
return;
}
// 获取当前结点的父结点
Node parentNode = searchParentNode(target);
// 删除的结点是叶子结点
if (targetNode.left == null && targetNode.right == null) {
// 判断是左结点还是右结点
if (parentNode.left != null && parentNode.left.val == target) {
parentNode.left = null;
} else {
parentNode.right = null;
}
return;
}
// 删除的结点有两个结点
if (targetNode.left != null && targetNode.right != null) {
// 从右子树找到最小的值并删除,将该值赋值给targetNode
targetNode.val = delRightTreeMin(targetNode.right);
return;
}
// 删除只有一颗子树的结点
if (targetNode.left != null) {
if(parentNode == null){
root = targetNode.left;
return;
}
// 当前结点存在左子树
if (parentNode.left.val == target) {
parentNode.left = targetNode.left;
} else {
parentNode.right = targetNode.left;
}
}
if (targetNode.right != null) {
if(parentNode == null){
root = targetNode.right;
return;
}
// 当前结点存在右子树
if (parentNode.right.val == target) {
parentNode.left = targetNode.right;
} else {
parentNode.right = targetNode.right;
}
}
}
private int delRightTreeMin(Node node) {
Node target = node;
// 循环的查找左子节点,就会找到最小值
while (target.left != null) {
target = target.left;
}
// 此时 target就指向了最小结点 删除最小结点(该节点肯定是左叶子节点)
delNode(target.val);
return target.val;
}
}
class Node {
int val;
Node left;
Node right;
public Node(int val) {
this.val = val;
}
// 查找结点
public Node search(int target) {
if (this.val == target) {
return this;
} else if (this.val > target) {
if (this.left == null) {
return null;
}
return this.left.search(target);
} else {
if (this.right == null) {
return null;
}
return this.right.search(target);
}
}
// 查找当前结点的父结点
public Node searchParentNode(int target) {
if ((this.left != null && this.left.val == target) || (this.right != null && this.right.val == target)) {
return this;
} else if (this.left != null && this.val > target) {
return this.left.searchParentNode(target);
} else if (this.right != null && this.val <= target) {
return this.right.searchParentNode(target);
} else {
return null;
}
}
// 添加结点
public void add(Node node) {
if (node == null) {
return;
}
// 如果当前待插入结点的值小于当前结点,将其插入在左子树中
if (node.val < this.val) {
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
} else {
// 将当前结点插入右子树
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
}
// 中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
@Override
public String toString() {
return "Node{" +
"val=" + val +
'}';
}
}
平衡二叉树
二叉搜索树一定程度上可以提高搜索效率,但是当序列构造二叉搜索树,可能会将二叉树退化成单链表,从而降低搜索效率。 平衡二叉树又称 AVL 树是一种自平衡的二叉排序树。它要求树中每个节点的左右子树高度差的绝对值不能超过1。通过这种方式,平衡二叉树保证了查找、插入和删除操作的时间复杂度始终保持在O(log n)级别。为了保持平衡,AVL树在插入或删除节点时,会通过旋转操作调整树的结构,以确保平衡性。
平衡二叉树最大的优点是能够保持较低的树高,从而保证了查找、插入和删除操作的高效性。由于它的高度差被限制在1,最坏情况下的时间复杂度仍为O(log n),避免了二叉排序树退化为链表的情况。 由于每次插入或删除节点后都可能需要进行旋转操作,平衡二叉树的实现比普通的二叉排序树要复杂。旋转操作可能导致额外的时间开销,特别是在大量数据操作时,旋转的次数也会增加。
平衡二叉树非常适用于对数据进行频繁查找、插入和删除的场景。它广泛应用于数据库的索引结构、操作系统的内存管理(如页表管理)、缓存系统等需要维持动态有序集合的应用中。
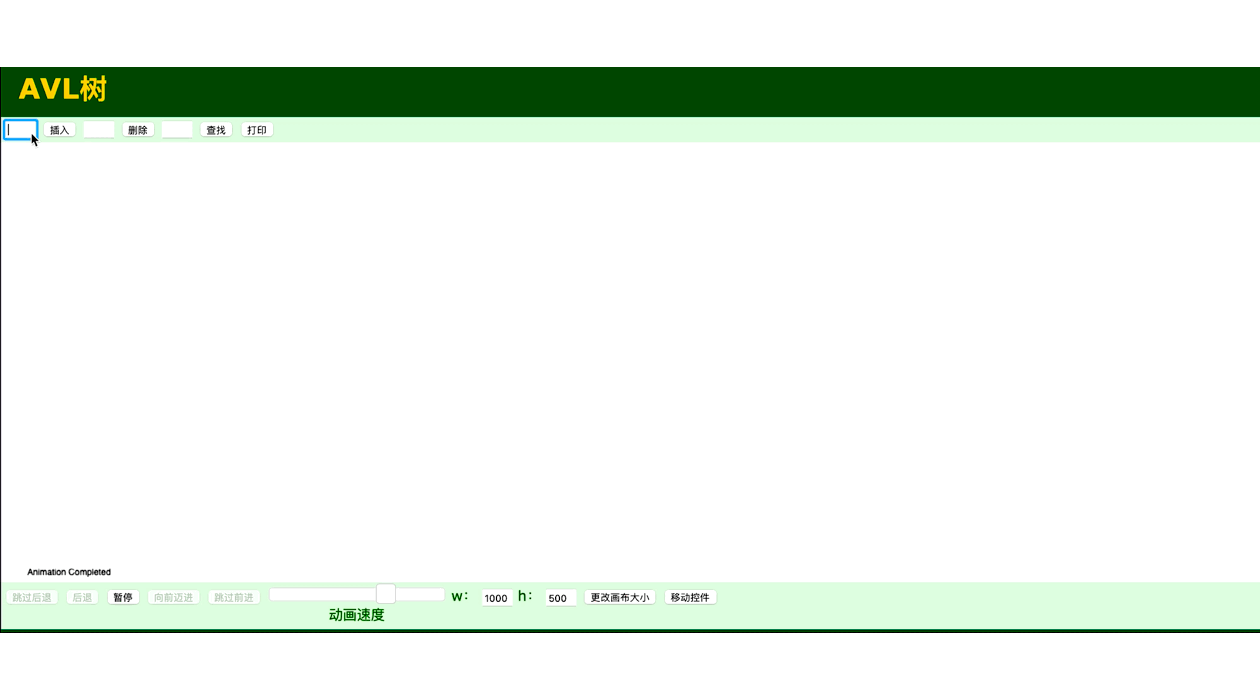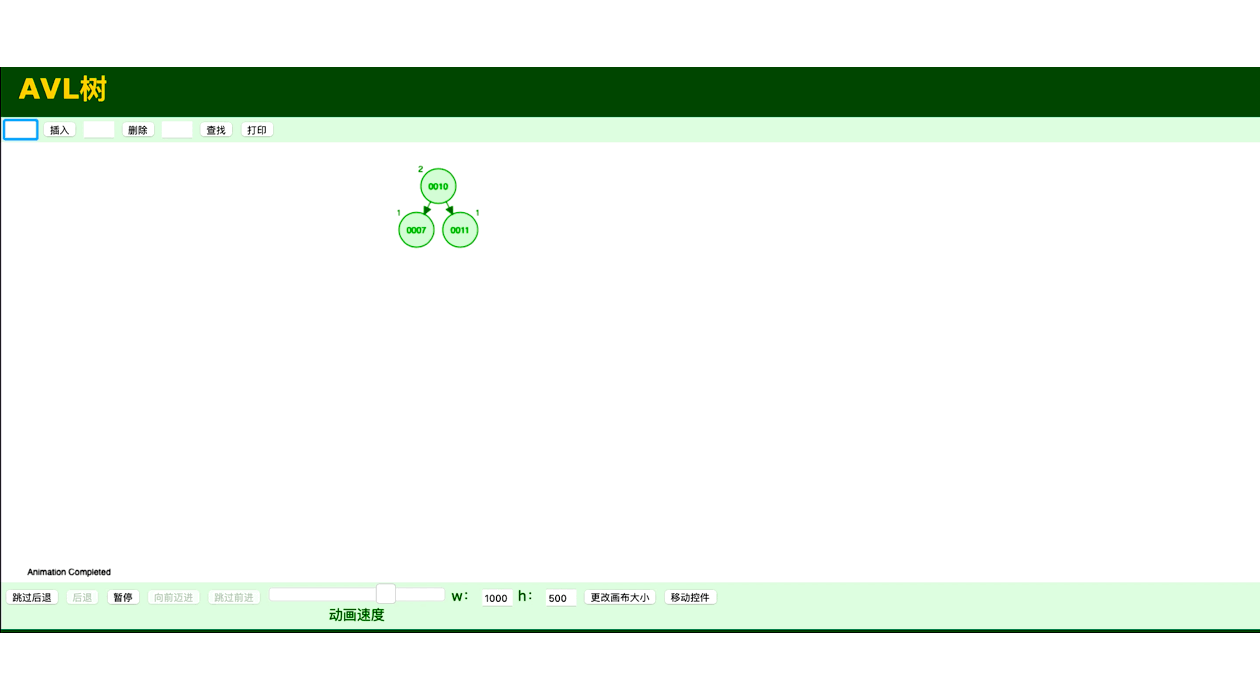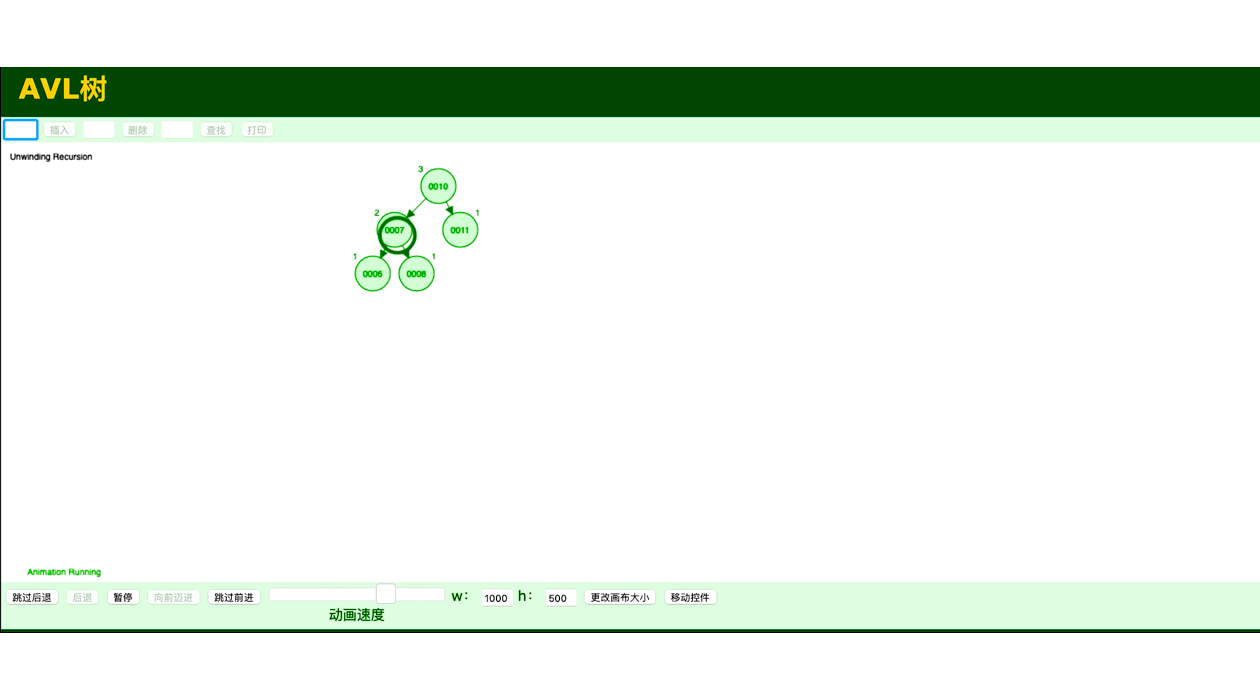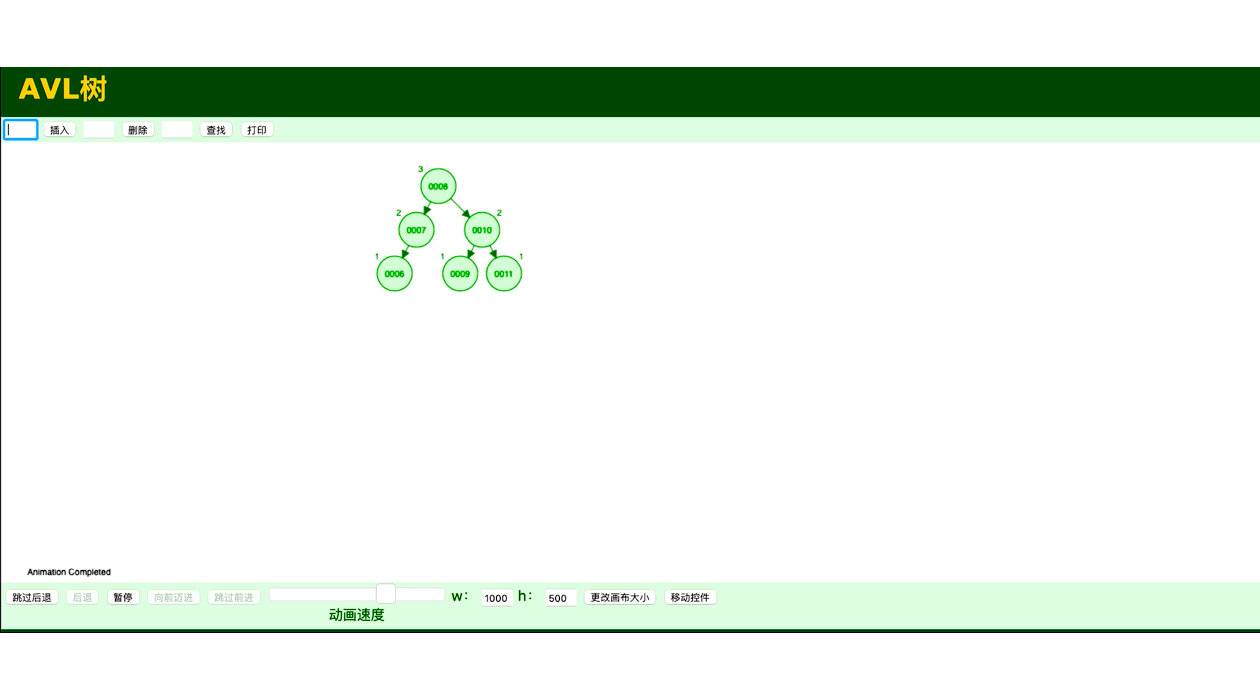
将有序二叉树变为平衡二叉树代码
public class AVLTreeDemo {
public static void main(String[] args) {
AVLTree avlTree = new AVLTree();
int[] arr = {10, 11, 7, 6, 8, 9 };
for (int i = 0; i < arr.length; i++) {
Node node = new Node(arr[i]);
avlTree.add(node);
}
System.out.println("当前树高度:"+ avlTree.height());
System.out.println("当前根结点:" + avlTree.getRoot());
System.out.println("当前左子树高度:"+ avlTree.getRoot().leftHeight());
System.out.println("当前右子树高度:"+ avlTree.getRoot().rightHeight());
}
}
class AVLTree{
private Node root;
public void setRoot(Node root) {
this.root = root;
}
public Node getRoot() {
return root;
}
public int height(){
if (root == null){
return 0;
}
return this.root.height();
}
// 添加结点
public void add(Node node) {
if (this.root == null) {
this.root = node;
} else {
this.root.add(node);
}
}
// 中序遍历
public void infixOrder() {
if (this.root != null) {
this.root.infixOrder();
}
}
}
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
// 获取当前左子树的高度
public int leftHeight(){
if (this.left == null){
return 0;
}
return this.left.height();
}
// 获取当前结点右子树的高度
public int rightHeight(){
if (this.right == null){
return 0;
}
return this.right.height();
}
// 获取当前结点的高度
public int height() {
return Math.max(
(this.left == null ? 0 : this.left.height()),
(this.right == null ? 0 : this.right.height())
) + 1;
}
// 左旋转
public void leftRote(){
// 创建一个新结点,并设置值等于当前结点的值
Node newNode = new Node(value);
// 使新结点的左结点指向当前结点的左结点
newNode.left = left;
// 新结点的右结点指向当前结点的右结点的左结点
newNode.right = right.left;
// 使当前结点的值指向新结点
value = right.value;
// 使当前结点的右结点指向当前结点的右结点的右结点
right = right.right;
// 使当前结点的左结点指向新结点
left = newNode;
}
// 右旋转
public void rightRote(){
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
// 添加结点
public void add(Node node) {
if (node == null) {
return;
}
// 如果当前待插入结点的值小于当前结点,将其插入在左子树中
if (node.value < this.value) {
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
} else {
// 将当前结点插入右子树
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
// 如果左子树的高度-右子树的高度 > 1 进行右旋转 反之进行左旋转
if (this.leftHeight() - this.rightHeight() > 1){
// 如果当前结点的左子树的右子树的高度>当前结点左子树的左子树的高度 则进行左旋转
if (this.left != null && this.left.rightHeight() > this.left.leftHeight()){
// 对当前结点的左结点进行左旋转
this.left.leftRote();
// 对当前结点右旋转
this.rightRote();
}else {
this.rightRote();
}
return;
}
if (this.rightHeight() - this.leftHeight() > 1) {
if (this.right != null && this.right.leftHeight() > this.right.rightHeight()){
// 对当前结点的右结点进行右旋转
this.right.rightRote();
// 对当前结点进行左旋转
this.leftRote();
}else {
this.leftRote();
}
}
}
// 中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
}
多路查找树
在二叉树中,每个节点有数据项,最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点,就是多叉树。多叉树通过重新组织节点,减少树的高度,能对二叉树进行优化。典型的多叉树有:2-3树、2-3-4树、红黑树和B树。
多叉树的前提是有序二叉树。
2-3树
2-3树是一种自平衡的多路查找树,是由二节点和三节点构成的树,是最简单的B树结构,2-3树的所有叶子节点都在同一层。
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点;
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点;
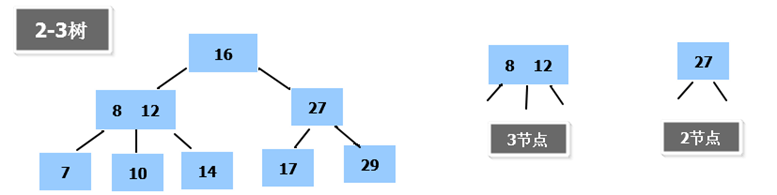
2-3树的最大优点是它始终保持平衡,保证了查找、插入和删除操作的时间复杂度为O(log n)。由于每个节点可以有2个或3个子节点,这减少了树的高度,进而减少了查找操作所需的时间。此外,2-3树本身不需要复杂的旋转操作,只要保证插入和删除过程中节点的分裂和合并。 2-3树的缺点在于插入和删除操作的实现较为复杂,尤其是在插入或删除时,可能需要将键从父节点传递到子节点或进行节点分裂。这些操作可能需要更多的计算和内存开销。另外,由于节点可以包含多个键,在某些情况下,节点的管理和内存访问效率较低。
2-3树适用于需要高效查找、插入和删除操作的场景,尤其是磁盘存储的数据库系统中,能够有效管理大量数据。它在文件系统、数据库索引、以及需要动态有序存储的应用中有广泛的应用。2-3树是B树和B+树的基础概念,理解2-3树有助于更好地理解其他更复杂的多路查找树结构。
2-3-4树,与2-3树类似,属于2-3树的扩展。
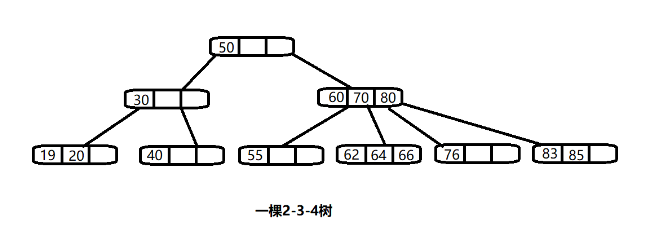
2-3-4树与2-3树的主要区别在于每个节点的存储能力。2-3树的节点最多包含2个子节点和1个键,而2-3-4树的节点可以包含3个子节点和2个键,最多可以有4个子节点和3个键。由于2-3-4树的每个节点能够存储更多的键,它的树高较低,相应地提高了查找、插入和删除操作的效率,特别是在处理大规模数据时。相比之下,2-3树的节点较少,树的高度可能较高,从而导致性能相对较低。尽管2-3-4树的节点管理更为复杂,但它在需要处理大量数据的系统中表现得更加高效,常用于数据库、文件系统等需要高效索引和数据存储的场景。
2-3树代码实现
class TreeNode {
int[] keys = new int[2]; // 存储最多2个键
TreeNode[] children = new TreeNode[3]; // 存储最多3个子节点
int numKeys = 0; // 当前节点的键数
// 构造器
public TreeNode() {
for (int i = 0; i < 3; i++) {
children[i] = null;
}
}
}
public class TwoThreeTree {
private TreeNode root;
// 构造器
public TwoThreeTree() {
root = new TreeNode();
}
// 插入操作
public void insert(int key) {
root = insert(root, key);
}
private TreeNode insert(TreeNode node, int key) {
if (node == null) {
node = new TreeNode();
node.keys[0] = key;
node.numKeys = 1;
return node;
}
if (node.numKeys < 2) {
insertInNode(node, key);
return null;
}
// Node is full, split it
TreeNode newRoot = new TreeNode();
splitNode(node, newRoot);
// Recurse into appropriate child
if (key < newRoot.keys[0]) {
insert(newRoot.children[0], key);
} else {
insert(newRoot.children[1], key);
}
return newRoot;
}
private void insertInNode(TreeNode node, int key) {
int i = node.numKeys;
while (i > 0 && node.keys[i - 1] > key) {
node.keys[i] = node.keys[i - 1];
i--;
}
node.keys[i] = key;
node.numKeys++;
}
private void splitNode(TreeNode node, TreeNode newRoot) {
newRoot.keys[0] = node.keys[1];
newRoot.numKeys = 1;
node.numKeys = 1;
newRoot.children[0] = node.children[0];
newRoot.children[1] = node.children[1];
newRoot.children[2] = node.children[2];
node.children[0] = null;
node.children[1] = null;
node.children[2] = null;
}
// 查找操作
public boolean search(int key) {
return search(root, key);
}
private boolean search(TreeNode node, int key) {
if (node == null) return false;
for (int i = 0; i < node.numKeys; i++) {
if (key == node.keys[i]) return true;
else if (key < node.keys[i]) return search(node.children[i], key);
}
return search(node.children[node.numKeys], key);
}
// 打印树结构(用于调试)
public void printTree() {
printTree(root, "", true);
}
private void printTree(TreeNode node, String indent, boolean last) {
if (node != null) {
System.out.println(indent + "+- " + node.keys[0] + " " + node.numKeys);
for (int i = 0; i < node.numKeys; i++) {
printTree(node.children[i], indent + " ", i == node.numKeys - 1);
}
}
}
public static void main(String[] args) {
TwoThreeTree tree = new TwoThreeTree();
tree.insert(10);
tree.insert(20);
tree.insert(5);
tree.insert(6);
tree.insert(15);
tree.insert(30);
tree.printTree();
System.out.println(tree.search(6)); // Output: true
System.out.println(tree.search(25)); // Output: false
}
}
B树
B树是一种自平衡的多路查找树,广泛用于数据库和文件系统中。它允许每个节点存储多个键,节点之间的子节点数量可变。B树通过分裂和合并节点来保持平衡,从而提高查找、插入和删除操作的效率。B树在需要高效磁盘存储和大数据集管理的场景中非常有用,尤其在减少磁盘IO操作方面表现优异。
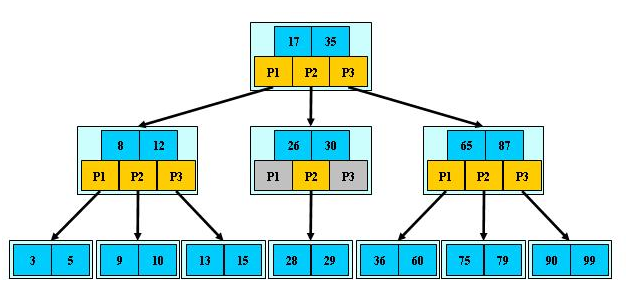
文件系统及数据库系统的设计者利用了磁盘预读原理,将一个节点的大小设为等于一个页(页的大小通常为4k),这样每个节点只需要一次IO就可以完全载入。
B树的阶(度):节点的最多子节点个数。比如2-3树的阶是3,2-3-4树的阶是4。
B树支持高效的查找、插入和删除操作,时间复杂度为 O(log n)。适用于大数据存储,能够减少磁盘IO操作。但实现较为复杂,节点分裂和合并时的处理需要较多计算。在某些情况下会浪费存储空间,尤其是节点不完全填满时。 B树常用于数据库索引、文件系统和其他需要高效查找、大规模数据存储的系统。在处理磁盘存储时,B树能有效减少读取次数,提升性能。
代码实现B树
class BTreeNode {
int[] keys;
BTreeNode[] children;
int numKeys;
boolean isLeaf;
// Constructor for BTreeNode
BTreeNode(int degree, boolean isLeaf) {
keys = new int[2 * degree - 1]; // Maximum number of keys
children = new BTreeNode[2 * degree]; // Maximum number of children
this.isLeaf = isLeaf;
numKeys = 0;
}
}
class BTree {
private BTreeNode root;
private int degree;
// Constructor for BTree
public BTree(int degree) {
this.degree = degree;
this.root = new BTreeNode(degree, true);
}
// Insert a key into the BTree
public void insert(int key) {
BTreeNode rootNode = root;
// If root is full, split it
if (rootNode.numKeys == 2 * degree - 1) {
BTreeNode newRoot = new BTreeNode(degree, false);
newRoot.children[0] = rootNode;
splitChild(newRoot, 0);
root = newRoot;
}
insertNonFull(root, key);
}
// Split the child of a node
private void splitChild(BTreeNode parent, int index) {
BTreeNode child = parent.children[index];
BTreeNode newChild = new BTreeNode(degree, child.isLeaf);
parent.children[index + 1] = newChild;
// Move half of the keys and children to the new node
for (int i = 0; i < degree - 1; i++) {
newChild.keys[i] = child.keys[i + degree];
}
if (!child.isLeaf) {
for (int i = 0; i < degree; i++) {
newChild.children[i] = child.children[i + degree];
}
}
child.numKeys = degree - 1;
newChild.numKeys = degree - 1;
// Insert the middle key into the parent node
for (int i = parent.numKeys; i > index; i--) {
parent.children[i + 1] = parent.children[i];
}
parent.children[index + 1] = newChild;
for (int i = parent.numKeys - 1; i >= index; i--) {
parent.keys[i + 1] = parent.keys[i];
}
parent.keys[index] = child.keys[degree - 1];
parent.numKeys++;
}
// Insert a key into a non-full node
private void insertNonFull(BTreeNode node, int key) {
int index = node.numKeys - 1;
if (node.isLeaf) {
// Find position to insert the key
while (index >= 0 && key < node.keys[index]) {
node.keys[index + 1] = node.keys[index];
index--;
}
node.keys[index + 1] = key;
node.numKeys++;
} else {
// Find child to insert into
while (index >= 0 && key < node.keys[index]) {
index--;
}
index++;
BTreeNode child = node.children[index];
if (child.numKeys == 2 * degree - 1) {
splitChild(node, index);
if (key > node.keys[index]) {
index++;
}
}
insertNonFull(node.children[index], key);
}
}
// Print the tree (for testing)
public void printTree() {
printTreeHelper(root, "", true);
}
private void printTreeHelper(BTreeNode node, String indent, boolean isLast) {
if (node != null) {
System.out.println(indent + "+- " + (node.isLeaf ? "Leaf" : "Internal") + " Node, Keys: " + java.util.Arrays.toString(java.util.Arrays.copyOf(node.keys, node.numKeys)));
indent += isLast ? " " : "| ";
for (int i = 0; i <= node.numKeys; i++) {
if (!node.isLeaf) {
printTreeHelper(node.children[i], indent, i == node.numKeys);
}
}
}
}
}
public class BTreeTest {
public static void main(String[] args) {
BTree bTree = new BTree(3); // Create B-tree of degree 3
// Insert keys into the B-tree
bTree.insert(10);
bTree.insert(20);
bTree.insert(5);
bTree.insert(6);
bTree.insert(12);
bTree.insert(30);
bTree.insert(7);
bTree.insert(17);
// Print the tree structure
bTree.printTree();
}
}
B+树
B+树是B树的一种变种,常用于数据库和文件系统中。与B树不同的是,B+树将所有的实际数据存储在叶子节点,而非叶子节点只存储键值。所有叶子节点通过指针连接起来,形成一个链表,使得范围查询更加高效。B+树支持高效的插入、删除和查找操作,能够有效地减少磁盘IO,并且对于大规模数据集具有更好的性能表现。
B+树通过将所有数据存储在叶子节点,并通过指针连接叶子节点形成链表,优化了范围查询操作。非叶子节点仅存储键,减少了存储开销。树的高度较低,查找、插入和删除操作的时间复杂度为 O(log n),即使在数据量庞大的情况下也能保持高效。 B+树的插入和删除操作较为复杂,需要调整节点结构,并可能涉及节点的分裂或合并,这使得这些操作相对耗时。叶子节点的链表结构增加了额外的空间开销。
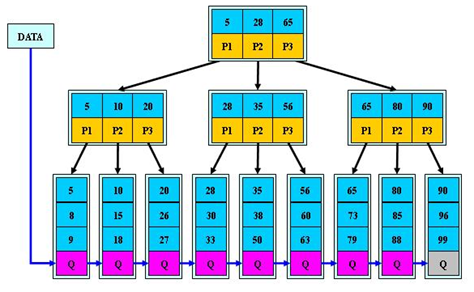
B+树被广泛应用于数据库索引和文件系统,尤其适合需要高效范围查询和顺序访问的场景,如文件存储和大数据处理。它在大规模数据的查找、插入和删除操作中表现出色,特别适合处理磁盘存储或分布式存储系统中的数据。
代码实现
class BPlusTreeNode {
int[] keys;
BPlusTreeNode[] children;
BPlusTreeNode next; // Pointer to the next leaf node (for range query)
boolean isLeaf;
int numKeys;
public BPlusTreeNode(int degree, boolean isLeaf) {
keys = new int[2 * degree - 1];
children = new BPlusTreeNode[2 * degree];
this.isLeaf = isLeaf;
numKeys = 0;
next = null; // Only used for leaf nodes
}
}
class BPlusTree {
private BPlusTreeNode root;
private int degree;
public BPlusTree(int degree) {
this.degree = degree;
this.root = new BPlusTreeNode(degree, true);
}
// Insert a key into the B+ tree
public void insert(int key) {
BPlusTreeNode rootNode = root;
if (rootNode.numKeys == 2 * degree - 1) {
BPlusTreeNode newRoot = new BPlusTreeNode(degree, false);
newRoot.children[0] = rootNode;
splitChild(newRoot, 0);
root = newRoot;
}
insertNonFull(root, key);
}
// Split the child of a node
private void splitChild(BPlusTreeNode parent, int index) {
BPlusTreeNode child = parent.children[index];
BPlusTreeNode newChild = new BPlusTreeNode(degree, child.isLeaf);
parent.children[index + 1] = newChild;
for (int i = 0; i < degree - 1; i++) {
newChild.keys[i] = child.keys[i + degree];
}
if (!child.isLeaf) {
for (int i = 0; i < degree; i++) {
newChild.children[i] = child.children[i + degree];
}
}
child.numKeys = degree - 1;
newChild.numKeys = degree - 1;
for (int i = parent.numKeys; i > index; i--) {
parent.children[i + 1] = parent.children[i];
}
parent.children[index + 1] = newChild;
for (int i = parent.numKeys - 1; i >= index; i--) {
parent.keys[i + 1] = parent.keys[i];
}
parent.keys[index] = child.keys[degree - 1];
parent.numKeys++;
}
// Insert a key into a non-full node
private void insertNonFull(BPlusTreeNode node, int key) {
int index = node.numKeys - 1;
if (node.isLeaf) {
while (index >= 0 && key < node.keys[index]) {
node.keys[index + 1] = node.keys[index];
index--;
}
node.keys[index + 1] = key;
node.numKeys++;
} else {
while (index >= 0 && key < node.keys[index]) {
index--;
}
index++;
BPlusTreeNode child = node.children[index];
if (child.numKeys == 2 * degree - 1) {
splitChild(node, index);
if (key > node.keys[index]) {
index++;
}
}
insertNonFull(node.children[index], key);
}
}
// Print the tree (for testing)
public void printTree() {
printTreeHelper(root, "", true);
}
private void printTreeHelper(BPlusTreeNode node, String indent, boolean isLast) {
if (node != null) {
System.out.println(indent + "+- " + (node.isLeaf ? "Leaf" : "Internal") + " Node, Keys: " + java.util.Arrays.toString(java.util.Arrays.copyOf(node.keys, node.numKeys)));
indent += isLast ? " " : "| ";
for (int i = 0; i <= node.numKeys; i++) {
if (!node.isLeaf) {
printTreeHelper(node.children[i], indent, i == node.numKeys);
}
}
}
}
}
public class BPlusTreeTest {
public static void main(String[] args) {
BPlusTree bTree = new BPlusTree(3); // Create B+ tree with degree 3
// Insert keys into the B+ tree
bTree.insert(10);
bTree.insert(20);
bTree.insert(5);
bTree.insert(6);
bTree.insert(12);
bTree.insert(30);
bTree.insert(7);
bTree.insert(17);
// Print the tree structure
bTree.printTree();
}
}
B*树
B*树是一种自平衡的多路查找树,它是B树的扩展。与B树相比,B*树在节点满时不仅会进行分裂,还会尝试从相邻的兄弟节点借用元素。如果借用成功,分裂操作会推迟,从而使得树的高度更加平衡。B*树通过这种策略减少了节点分裂的频率,优化了内存和磁盘的使用。
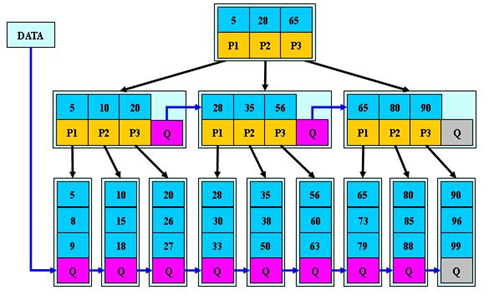
B*树能够通过减少节点的分裂操作,保持较低的树高度,这有助于减少磁盘访问次数和提高存储空间的利用率。它在存储容量较大的环境中表现优秀,特别适合需要高效查找和存储操作的场景。 但是B*树的插入和删除操作较为复杂,因为它涉及借用兄弟节点的元素和节点分裂。管理和维护树的平衡比B树更为复杂,因此实现起来较为麻烦,且在某些情况下可能导致更高的维护开销。
B*树常用于大规模数据存储系统,如数据库索引和文件系统,特别是在磁盘存储中,能够有效减少磁盘IO次数。它适用于需要大量存储和高效数据访问的应用,能够提升查询性能和存储空间的利用率。
代码实现
class BStarTree {
private static final int MIN_DEGREE = 3; // 阶数,控制树的分裂
private Node root;
public BStarTree() {
root = new Node(true);
}
// 节点类
class Node {
int[] keys;
Node[] children;
int keyCount;
boolean isLeaf;
public Node(boolean isLeaf) {
this.isLeaf = isLeaf;
this.keys = new int[2 * MIN_DEGREE - 1];
this.children = new Node[2 * MIN_DEGREE];
this.keyCount = 0;
}
}
// 插入操作
public void insert(int key) {
Node rootNode = root;
if (rootNode.keyCount == 2 * MIN_DEGREE - 1) { // 根节点满了
Node newRoot = new Node(false);
newRoot.children[0] = rootNode;
splitChild(newRoot, 0);
root = newRoot;
}
insertNonFull(root, key);
}
// 在非满节点中插入键
private void insertNonFull(Node node, int key) {
int i = node.keyCount - 1;
if (node.isLeaf) {
while (i >= 0 && key < node.keys[i]) {
node.keys[i + 1] = node.keys[i];
i--;
}
node.keys[i + 1] = key;
node.keyCount++;
} else {
while (i >= 0 && key < node.keys[i]) {
i--;
}
i++;
if (node.children[i].keyCount == 2 * MIN_DEGREE - 1) {
splitChild(node, i);
if (key > node.keys[i]) {
i++;
}
}
insertNonFull(node.children[i], key);
}
}
// 分裂子节点
private void splitChild(Node parent, int i) {
Node fullChild = parent.children[i];
Node newChild = new Node(fullChild.isLeaf);
parent.children[i + 1] = newChild;
parent.keys[i] = fullChild.keys[MIN_DEGREE - 1];
parent.keyCount++;
for (int j = 0; j < MIN_DEGREE - 1; j++) {
newChild.keys[j] = fullChild.keys[j + MIN_DEGREE];
}
if (!fullChild.isLeaf) {
for (int j = 0; j < MIN_DEGREE; j++) {
newChild.children[j] = fullChild.children[j + MIN_DEGREE];
}
}
fullChild.keyCount = MIN_DEGREE - 1;
}
// 打印树的内容
public void printTree() {
printTree(root, 0);
}
private void printTree(Node node, int level) {
if (node != null) {
System.out.println("Level " + level + " : ");
for (int i = 0; i < node.keyCount; i++) {
System.out.print(node.keys[i] + " ");
}
System.out.println();
if (!node.isLeaf) {
for (int i = 0; i <= node.keyCount; i++) {
printTree(node.children[i], level + 1);
}
}
}
}
public static void main(String[] args) {
BStarTree tree = new BStarTree();
tree.insert(10);
tree.insert(20);
tree.insert(5);
tree.insert(6);
tree.insert(12);
tree.insert(30);
tree.insert(7);
tree.insert(17);
tree.printTree();
}
}
图
图是一种由节点和连接节点的边组成的数据结构,其中结点可以具有零个或多个相邻元素。两个结点之间的连接称为边。结点也可以称为顶点。 如果给图的每条边规定一个方向,那么得到的图称为有向图。在有向图中,与一个节点相关联的边有出边和入边之分。相反,边没有方向的图称为无向图。
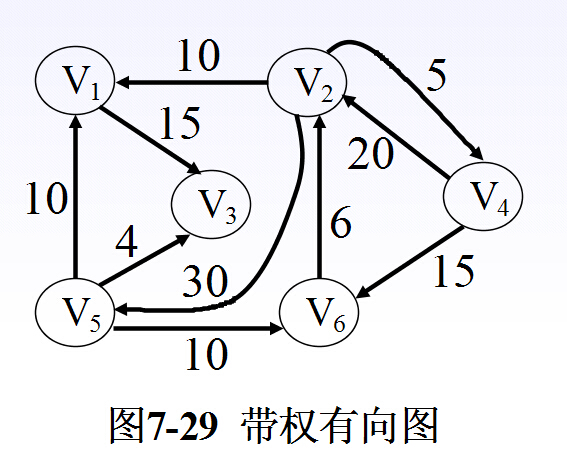
可用二维数组表示图(邻接矩阵)或链表表示(邻接表)。
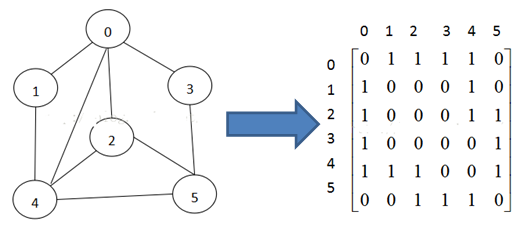
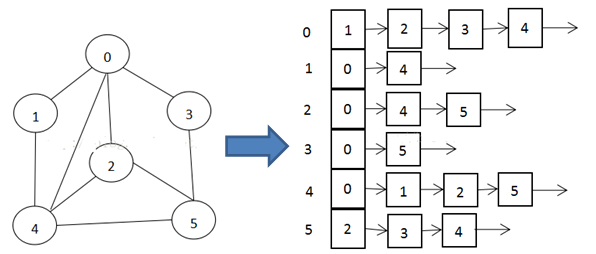
图能够灵活地表示复杂的关系和连接方式。它可以表示一对多、多对多的关系,比传统的线性结构如链表、数组更为适用,尤其是在处理具有复杂连接模式的数据时,如社交网络、路由图等。通过不同的遍历算法,可以高效地找到节点间的最短路径或遍历所有可能的路径。
图的存储和操作相对复杂。对于稠密图,边的数量远大于节点,存储开销较大。图的算法实现较为复杂,需要更多的计算资源和时间,特别是在涉及到图的遍历、路径查找、最短路径算法等问题时。随着图的规模增大,性能问题变得更加显著。
图常用于表示有复杂连接关系的问题,如社交网络中的朋友关系、地图中不同地点的距离、计算机网络中的设备连接等。在推荐系统、路径规划、流量控制等场景中,图也具有重要的应用。图特别适合用于需要描述多点间复杂关系的领域,如计算机网络拓扑、网页链接分析等。
代码模拟图,包括图的深度遍历,广度遍历:
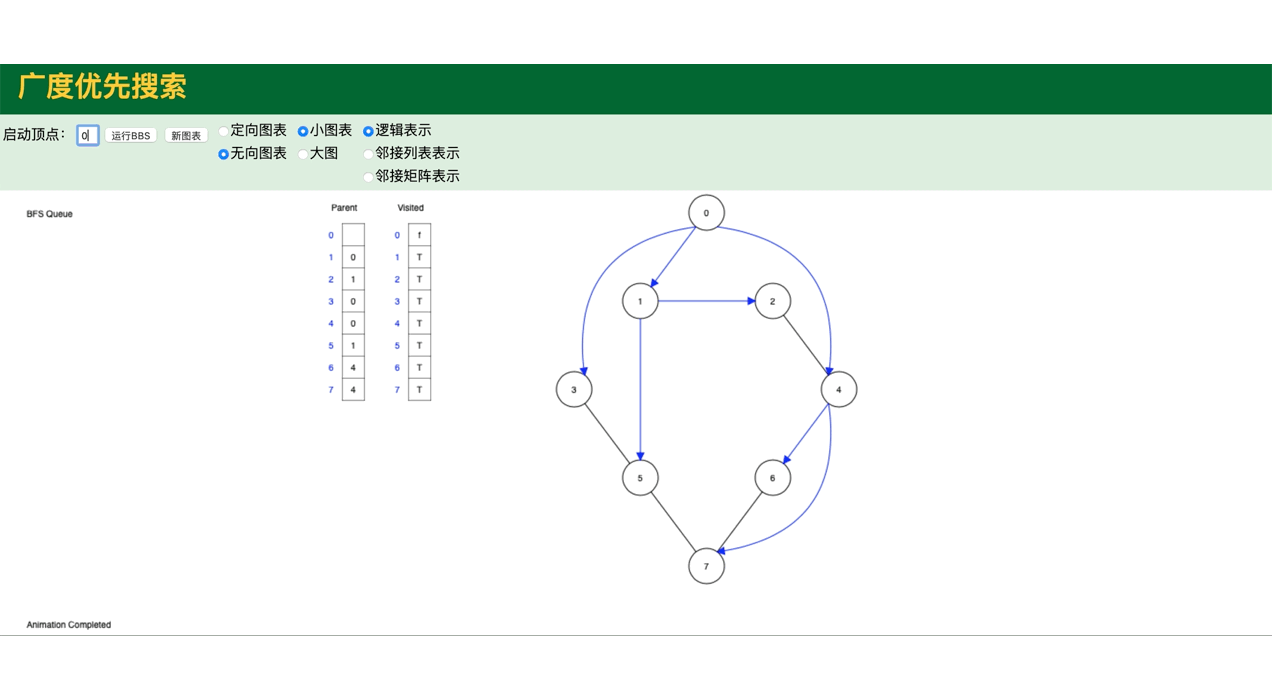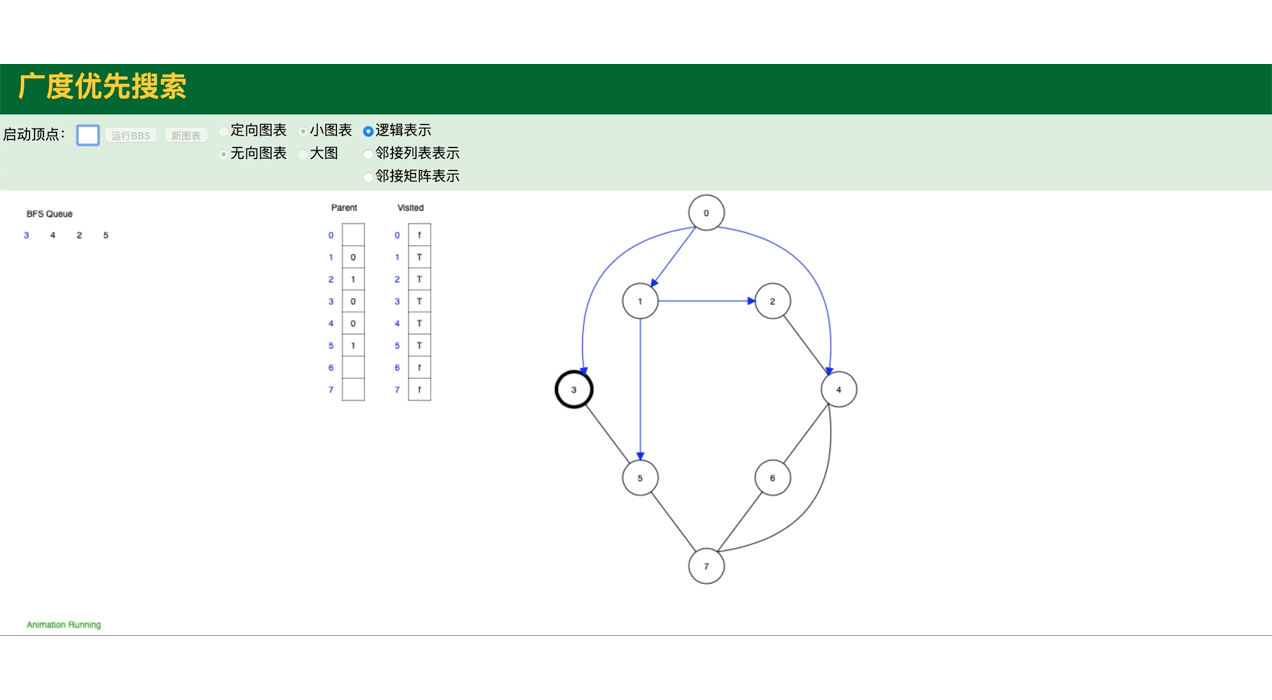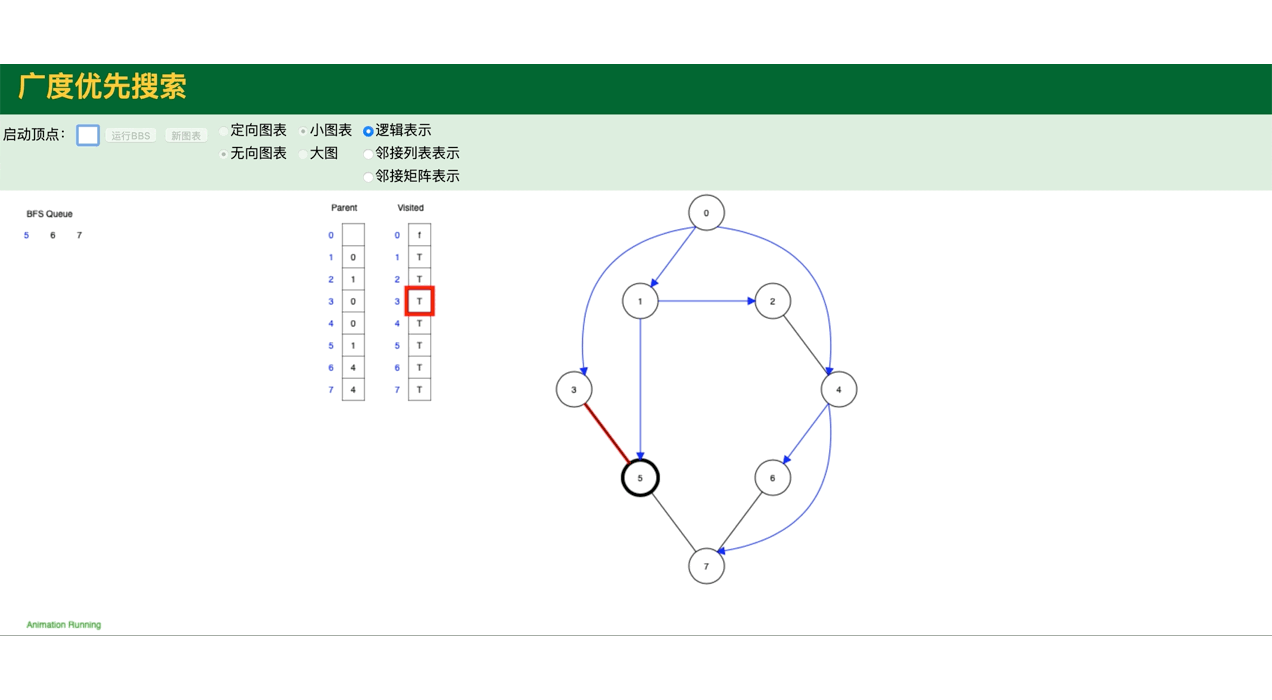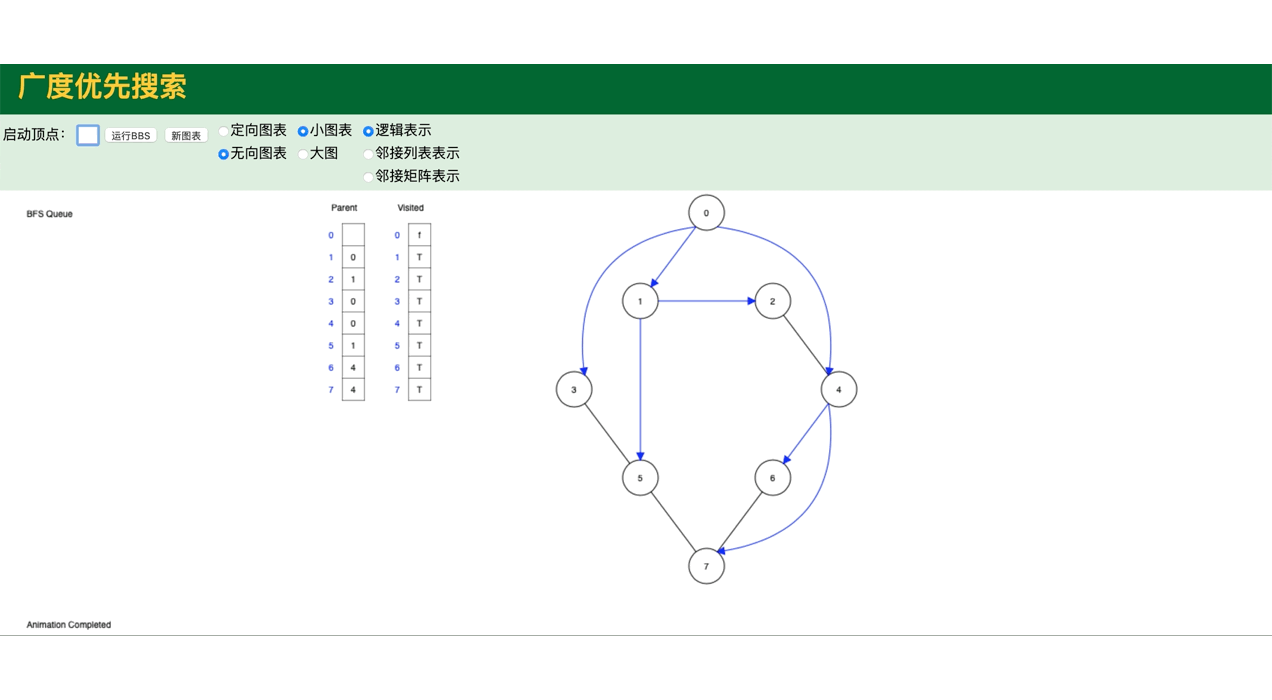
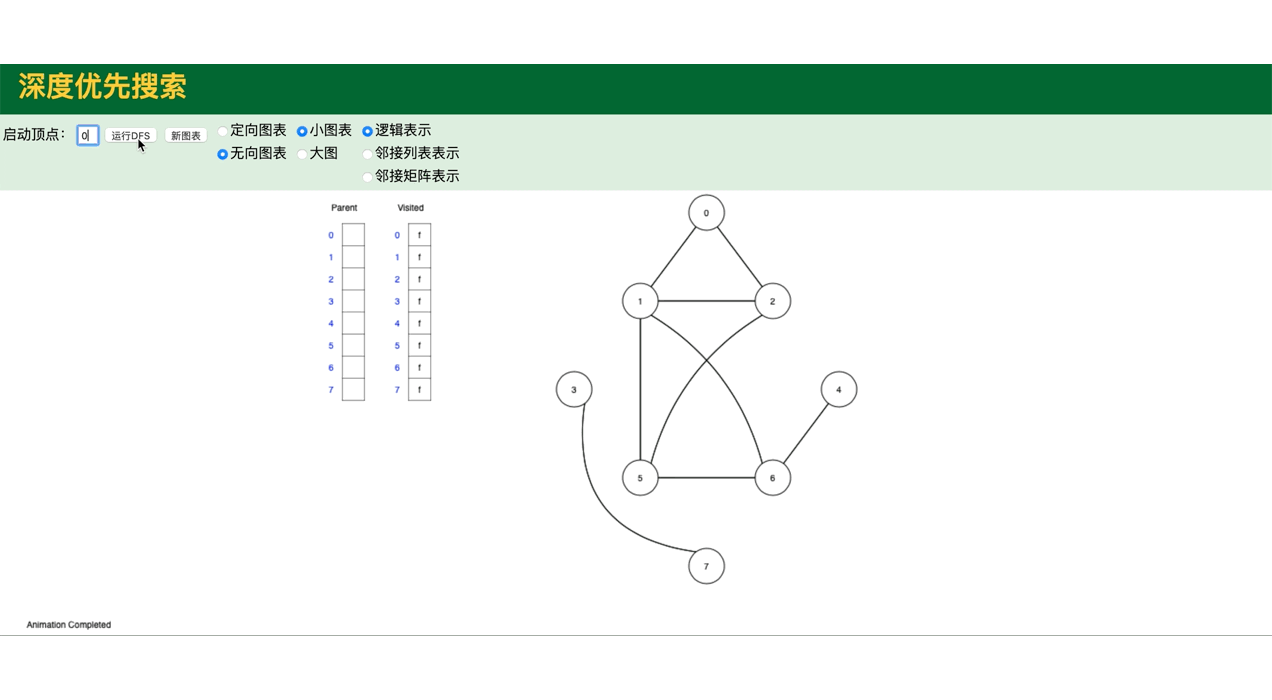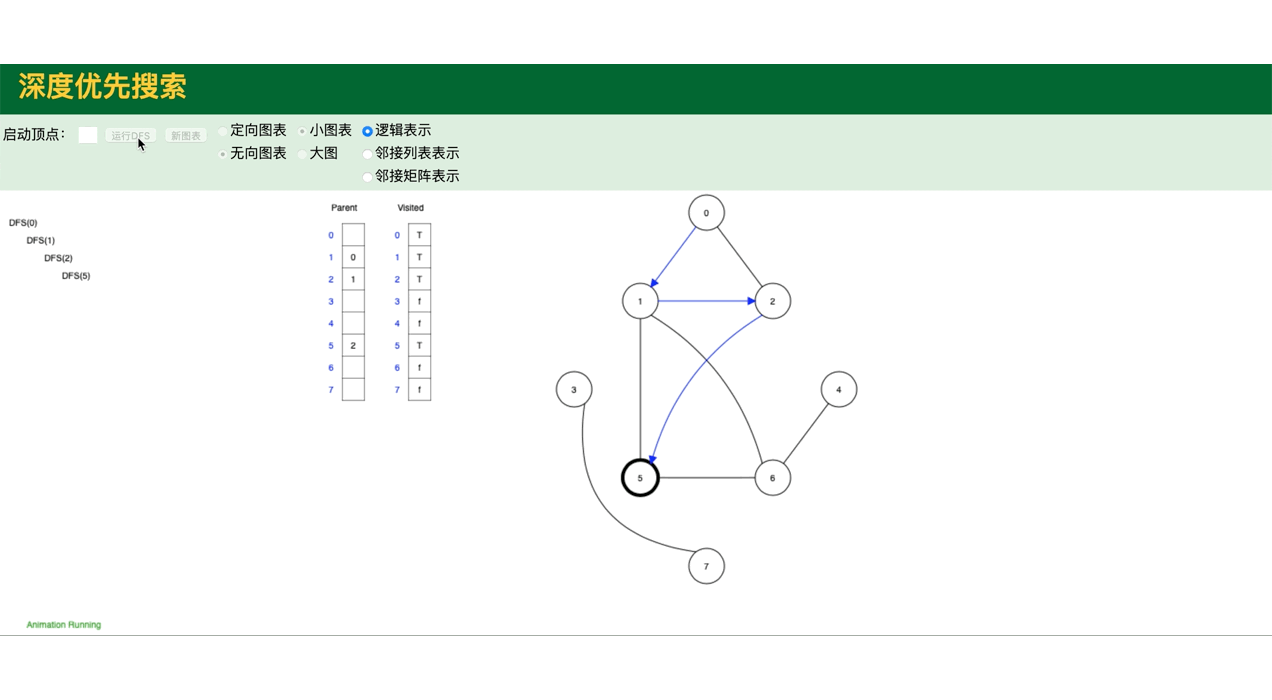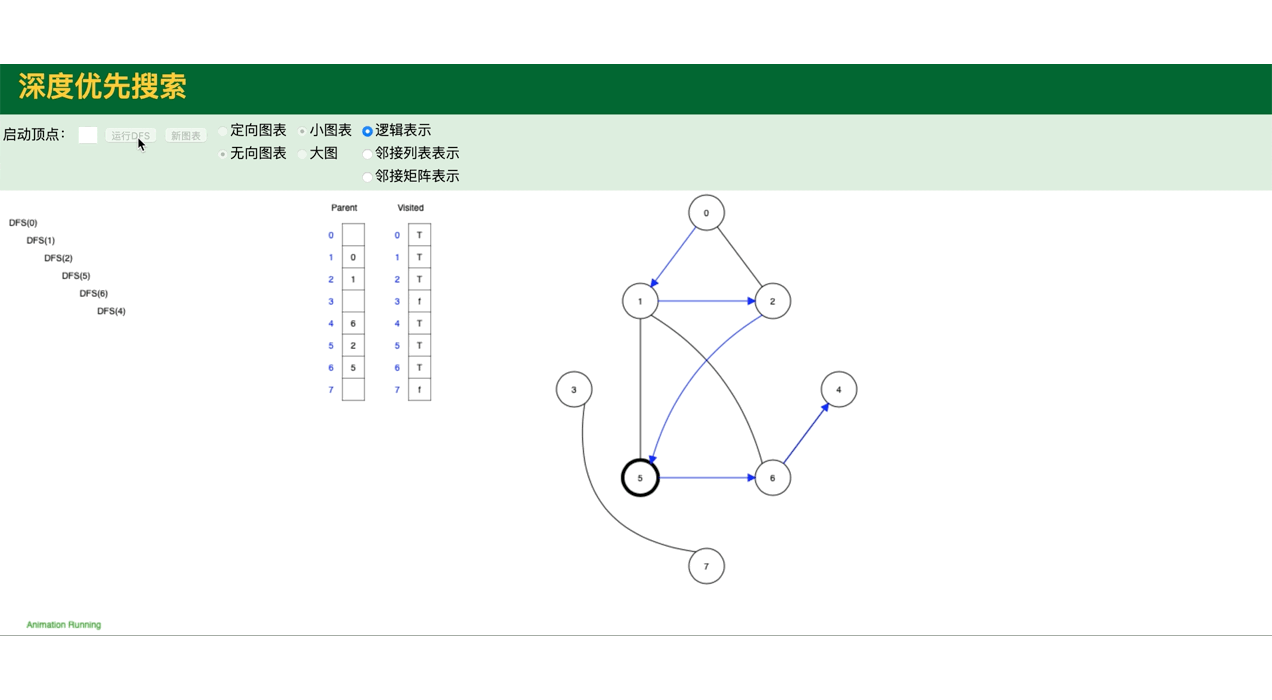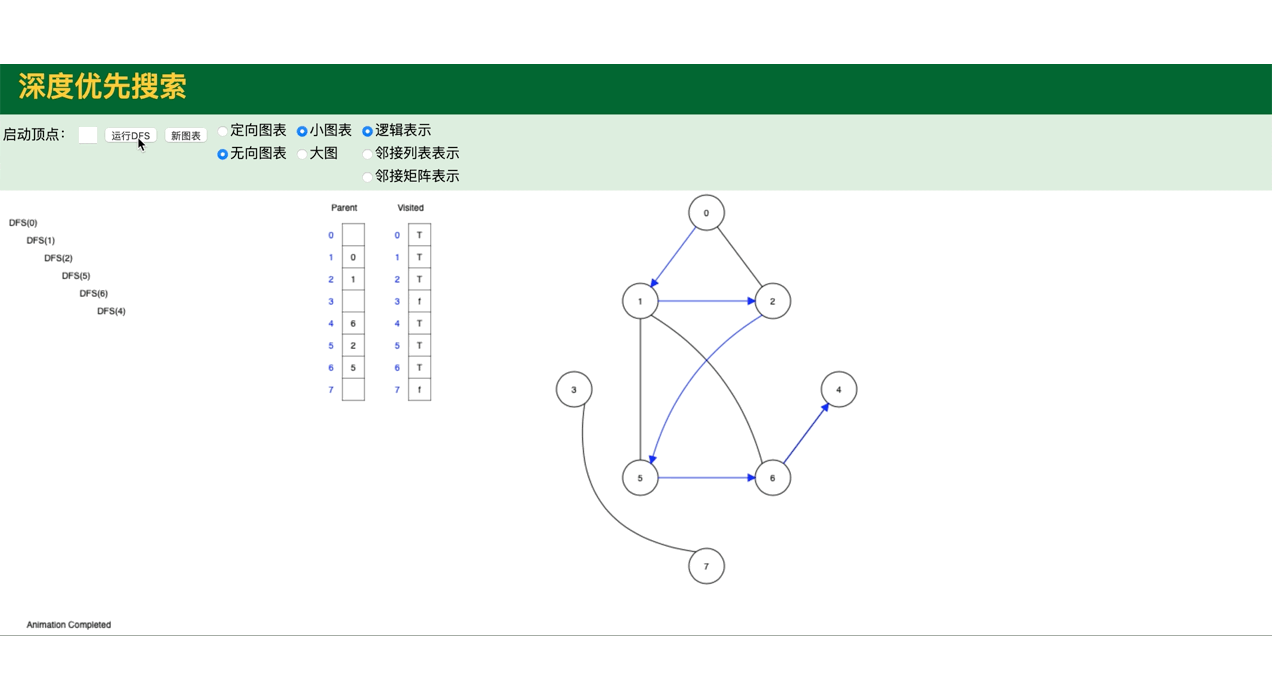
public class GraphDemo {
public static void main(String[] args) {
String[] vertexes = {"A", "B", "C", "D", "E"};
int n = vertexes.length;
Graph graph = new Graph(n);
for (String vertex : vertexes) {
graph.addVertex(vertex);
}
graph.addEdge(0, 1, 1); // A-B
graph.addEdge(0, 2, 1); // A-C
graph.addEdge(1, 2, 1); // B-C
graph.addEdge(1, 3, 1); // B-D
graph.addEdge(1, 4, 1); // B-E
// 展示图转换的矩阵
graph.showEdges();
// 图的深度遍历
graph.dfs();
System.out.println();
// 图的广度遍历
graph.bfs();
}
}
class Graph {
// 保存顶点
private List<String> vertexList;
// 保存边的数量
private int sideNums;
// 保存图的矩阵
private int[][] edges;
private boolean[] isVisited;
public Graph(int n) {
vertexList = new ArrayList<>(n);
edges = new int[n][n];
sideNums = 0;
}
// 获取第一个结点的下一个结点
private int getFirstNeighbor(int index) {
for (int i = 0; i < vertexList.size(); i++) {
if (edges[index][i] > 1) {
return i;
}
}
return -1;
}
// 获取当前结点的下一个结点
private int getNextNeighbor(int vertex, int index) {
for (int i = vertex + 1; i < vertexList.size(); i++) {
if (edges[index][i] > 1) {
return i;
}
}
return -1;
}
// 图的深度遍历
private void dfs(boolean[] isVisited, int i) {
System.out.print(getVertexValByIndex(i) + "->");
// 将当前遍历后的顶点标记为true
isVisited[i] = true;
// 获取当前结点的下一个结点的索引位置
int firstNeighborIndex = getFirstNeighbor(i);
// 如果 != -1 代表当前结点没有找到下一个结点,需要向下移动
while (firstNeighborIndex != -1) {
// 判断该结点是否被遍历过
if (!isVisited[firstNeighborIndex]) {
dfs(isVisited, firstNeighborIndex);
}
// 当前结点向后移动,否则是死循环
firstNeighborIndex = getNextNeighbor(firstNeighborIndex, i);
}
}
public void dfs() {
isVisited = new boolean[vertexList.size()];
for (int i = 0; i < getVertexCount(); i++) {
if (!isVisited[i]) {
dfs(isVisited, i);
}
}
}
// 一个结点的广度优先遍历
private void bfs(boolean[] isVisited, int i) {
// 队列头结点下标索引
int headIndex;
// 相邻结点下标索引
int neighborIndex;
LinkedList<Integer> queue = new LinkedList<>();
System.out.print(getVertexValByIndex(i) + "->");
isVisited[i] = true;
queue.addLast(i);
// 如果队列不等于空 则需要遍历循环查找
while (!queue.isEmpty()) {
headIndex = queue.removeFirst();
// 得到第一个邻接结点的下标
neighborIndex = getFirstNeighbor(headIndex);
while (neighborIndex != -1) {
// 是否访问过
if (!isVisited[neighborIndex]) {
System.out.print(getVertexValByIndex(neighborIndex) + "->");
isVisited[neighborIndex] = true;
queue.addLast(neighborIndex);
}
// neighborIndex 向下找
neighborIndex = getNextNeighbor(headIndex, neighborIndex);
}
}
}
// 广度优先遍历
public void bfs() {
isVisited = new boolean[vertexList.size()];
for (int i = 0; i < getVertexCount(); i++) {
if (!isVisited[i]) {
bfs(isVisited, i);
}
}
}
// 添加顶点
public void addVertex(String vertex) {
vertexList.add(vertex);
}
// 添加边
public void addEdge(int vertex1, int vertex2, int weight) {
edges[vertex1][vertex2] = weight;
edges[vertex2][vertex1] = weight;
sideNums++;
}
// 获取边的数量
public int getSideNums() {
return sideNums;
}
// 遍历矩阵
public void showEdges() {
for (int[] edge : edges) {
System.out.println(Arrays.toString(edge));
}
}
// 获取顶点数量
public int getVertexCount() {
return vertexList.size();
}
// 获取边之间的权值
public int getVertexWeight(int vertex1, int vertex2) {
return edges[vertex1][vertex2];
}
// 根据下标获取结点的值
public String getVertexValByIndex(int index) {
return vertexList.get(index);
}
}